[科普中国]-半瘦

半瘦（semi-thinness）是描述集合在某一点的邻域“稀薄”程度的一个概念。

简介半瘦是描述集合在某一点的邻域“稀薄”程度的一个概念。

设Ω为格林空间且Ω⊂Rn，对x0∈Ω，令称集E在x0半瘦指的是n→∞时，对每个t∈(0,1)成立。对于Ω⊂R2，这个条件等价于E∩En的外容量趋于零。

推广把Ω\E在E的每一点都半瘦的集E定义为半细开集，就得到半细拓扑。

半细拓扑下的极限称为半细极限。1

瘦性是描述一个点集在某一点的邻域充分“稀薄”的一个概念。

在拓扑空间(Ω,𝒥)中，取定一族从(Ω,𝒥)到(0,+∞)的下半连续函数组成的凸锥Φ，Ω的子集E称为在x0∉E瘦，指的是x0∉Ē（𝒥闭包），或x0∉Ē但存在u∈Φ，使得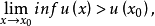其中x∈E。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所