[科普中国]-对数容量

对数容量(logarithmic capacity)是由对数核确定的一种容量。在R中，关于对数核考虑紧集F的倒容量Wl(F)，当限制F包含于单位圆B内时，若Wl(F)>0，则把1/Wl(F)称为F的维纳容量。

概念对数容量(logarithmic capacity)是由对数核确定的一种容量。在R中，关于对数核考虑紧集F的倒容量Wl(F)，当限制F包含于单位圆B内时，若Wl(F)>0，则把1/Wl(F)称为F的维纳容量。对一般紧集F，Wl(F)可能取0值或负值，要做类似的处理不方便，故定义：

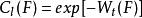为F的对数容量.对F⊂B，两种容量值相差甚大，但两种零容集等价，都是全不连通的勒贝格零集。值得注意的是，包含于区间[0，1]的康托尔三分集是勒贝格零集，但具有正的对数容量。当Cl(F)>0时，对R\F的无界分支上以无穷远点为极的格林函数g(z，∞)，极限

存在，称为鲁宾常数，它正好等于Wl(F)。1

容量容量是刻画巴拿赫空间中紧集的“大小”或“粗细”的一个不变量。设X是巴拿赫空间，A是X的一个紧子集。‖x‖是x∈X的范数，是给定的正数，y1，y2，…，ym是A中的m个点，如果它们中每两点之间的距离都超过ε，也即i≠k(i，k=1，2，…，m)时ρ(yi，yk)=‖yi-yk‖>ε，则称点组{yk}k=1是ε-分离的.自然，对给定的ε>0，ε-分离的点组{yk}k=1的点的个数与这些点的取法有关。但其最大值Mε(A)=maxm却是集A的一个不变量，Cε(A)=logMε(A)称为A的容量。Cε(A)关于A是单调递增的而关于ε则是单调递减的.在函数逼近论中，主要是对一些函数类考虑其容量在ε→0时的渐近性态及其应用。它开始于20世纪50年代。

容量与熵之间有如下关系：若X是巴拿赫空间，A是X的紧子集，则对ε>0有不等式：

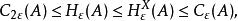其中Cε(A)是A的容量，Hε(A)是A的熵，Hε(A)是A关于X的熵。

对数位势对数位势是一般位势的经典模型之一。在R中，以K(x，y)=-log|x-y|为核(称为对数核)的位势称为对数位势，记为Ul。对数核是对称的、平移不变的，但不是正核.二维引力场的位势即为对数位势。

位势论现代分析数学领域的一个分支，主要研究各种形式的位势(函数)和与其密切关联的调和函数、上(下、超、次)调和函数族的各种性质及其应用。经典位势论的主要研究工具是微积分，并与微分方程、复变函数论紧密关联;现代位势论以拓扑、泛函分析与测度论、广义函数等为主要工具，与分析数学领域的诸多分支相互渗透并和随机过程建立了深刻的内在联系。位势论起源于物理学的万有引力学说和静电学，远在1733年，拉格朗日(Lagrange，J.-L.)就注意到引力场是一个函数(称为牛顿位势)的梯度。

1925年，里斯(Riesz，F.)引进了上(下)调和函数的概念，为位势论研究提供了新的方法；里斯分解定理建立了上调和函数与位势之间的紧密联系；而对上调和函数连续性的研究导致了细拓扑概念的引入。1

20世纪30年代，瓦莱·普桑(Vallée-Poussin，C.-J.-G.-N.de la)用现代观点改进并发展了庞加莱扫除法；弗罗斯特曼(Frostman，O.)发展了高斯变分法，成功地解决了紧集的平衡问题和扫除问题。同期，位势论已推广到非古典核的情况，特别是里斯位势核，它已不属于通常与偏微分方程关联的位势核了。

从20世纪40年代起，泛函分析、拓扑学的方法被系统地引入位势论并使它发展到一个新水平。1941年，嘉当(Cartan，H.)利用希尔伯特空间理论研究具有有限能量的测度等，得到很大成功；同年，马丁(Martin，R.S.)建立了马丁边界理论，导致了关于一般理想边界的深入研究；1950年，戴尼(Deny，J.)用广义函数论解决了完备化问题;1955年，绍凯(Choquet，G.)建立了一般容量理论及可容性定理，并用凸锥极端点理论改进了马丁的成果.此外，对于更一般空间(例如流形、LCA群)和更一般位势核的位势论也有了深入的探讨。

近30多年来，位势论迅速发展，其显著特点之一是各种公理体系的建立.为统一处理已有的理论并加以推广使之适用于一般椭圆型和抛物型方程或随机过程，自20世纪50年代中期起，陶茨(Tautz，G.)、杜布(Doob，J.L.)、布雷洛、鲍尔(Bauer，H.)、邦尼(Bony，J.M.)、康斯坦丁斯库(Constantinescu，C.)和柯尼(Cornea，A.)等人分别提出了不同的公理系统，建立各种形式的调和空间位势论(最近，关于多重调和空间及非线性位势论的公理系统也先后建立起来)；而戴尼和博灵(Beurling，A.)等人则从能量和狄利克雷积分等概念出发建立了狄利克雷空间论。位势论发展的另一个显著特点是，越来越广泛深入地与相邻分支，如复分析(包括黎曼曲面)、拓扑学、几何测度论、微分几何、微分方程、调和分析等相互结合和渗透，且发挥日益明显的作用与影响。特别引人注目的是，对于它与随机过程论之深刻联系的深入研究，同时促进了这两个分支的繁荣和发展，在杜布、亨特(Hunt，G.A.)、迈耶(Meyer，P.A.)和钟开莱等人出色工作的基础上，产生了所谓概率位势论或马尔可夫过程位势论，与此有关的课题正吸引着大批学者去做深入研究。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学