[科普中国]-格林线

设区域D的格林函数为G(x,a)，a为D中某个取定的点，那么它的正交轨线称为格林线。

简介格林线是格林函数的等位面的正交轨线。

设区域D的格林函数为G(x,a)，a为D中某个取定的点，那么它的正交轨线称为格林线。

性质对a的充分小邻域内的每一点x0(x0≠a)，有惟一的格林线经过它，这种格林线惟一对应着从a处出发与该格林线相切的射线，这种对应给出了从a点发出的格林线全体与射线全体之间的一一映射，其中从a发出的格林线，若在其上满足inf G=0，则此格林线称为正则的。因此，从a发出的格林线几乎都是正则的，即其中非正则者所对应的射线与球面S(a,C)={x||x-a|=C}的交是(n-1)维的勒贝格零测集。

此外，存在一个n维勒贝格零测集N，包含了临界点全体N，使在每一点x1∈D\N有惟一的正则格林线Γ经过。

推广让x1与r=G(x1,a)及Γ在a的单位切向量l组成的有序对(r,l)建立对应，就得到D\N中的格林坐标系，(r,l)称为x1的格林坐标。它是研究格林区域上的位势的重要工具。

若用s表示Γ从a到x1处的弧长，那么有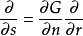在D\N成立，此处∂G/∂n表示等位面在x1处的外法向导数。1

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学