冯·诺伊曼和摩根斯坦恩在1944年提出了稳定集这个解概念。
对博弈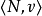 的分配集
的分配集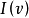 的一个子集
的一个子集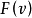 ,
,
(1) 如果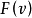 中的任何两个分配都没有优超关系(即不存在一个分配通过一个联盟占优另一个分配),则称
中的任何两个分配都没有优超关系(即不存在一个分配通过一个联盟占优另一个分配),则称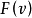 是内部稳定的。
是内部稳定的。
(2) 如果任取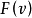 外的一个分配
外的一个分配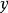 ,存在分配
,存在分配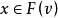 ,使得
,使得 优超
优超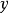 ,则称
,则称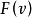 是外部稳定的。既是内部稳定的,又是外部稳定的分配集称为稳定集(也称为N-M解,诺伊曼-莫根施特恩解)2。
是外部稳定的。既是内部稳定的,又是外部稳定的分配集称为稳定集(也称为N-M解,诺伊曼-莫根施特恩解)2。
定理 核心必定属于稳定集,但稳定集不一定是核心。
核心里的任一个分配都不被其他分配优超,所以核心一定满足内部稳定,如果核心中有一个分配 不属于稳定集,则稳定集里一定存在一个分配
不属于稳定集,则稳定集里一定存在一个分配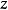 优超分配
优超分配 ,这与核心中的任一分配不被优超矛盾,所以核心属于稳定集2。
,这与核心中的任一分配不被优超矛盾,所以核心属于稳定集2。
有一家商店在搞打折促销的活动,优惠的方法是:单买一件棉衣100元;如果一次购买2件棉衣,第二件半价,即只要150元,但没有其他形式的优惠.现恰有互不相识的甲、乙、丙3人在店里都想买一件棉衣,则他们如果两个人合作,两人总共可以少花50元,如果3个人合作,也只可以节省50元,讨论该问题的稳定集。
解: 这个博弈的特征函数可以写为
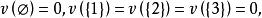
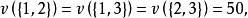
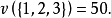
一个博弈可能形成哪一个联盟,这要考虑这个博弈所面对的现实环境的多种因素,如本题这个简单的例子,对于两人联盟,联盟外的第三个局中人会设法(如给联盟中一个局中人更高的收益)使一个局中人脱离原联盟与自己组成联盟。而三个人的联盟与两个人的联盟的收益一样多,三个人结成的大联盟更有问题,前面已经假设一个联盟形成后,在整个博弈过程中不变,因此形成了三人大联盟,就假设三人大联盟在分析时不破裂,注意这是决策的分析,不是现实中的实施,分析要全面,只有分析全面了,现实中的实施才更有保障。
这个博弈例子没有核心。
分配集的一个子集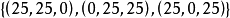 就是这个博弈的一个稳定集
就是这个博弈的一个稳定集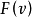 。因为这个集合中的任两个分配之间不存在优超关系。对集合外的一分配,例如
。因为这个集合中的任两个分配之间不存在优超关系。对集合外的一分配,例如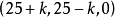 ,这里
,这里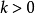 。分配
。分配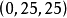 中关于联盟
中关于联盟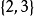 优超分配
优超分配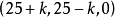 。
。
现对稳定集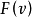 外的任一分配
外的任一分配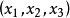 。因为是分配,所以
。因为是分配,所以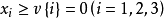 ,假设稳定集中的三个分配都不优超分配
,假设稳定集中的三个分配都不优超分配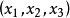 。
。
分配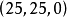 不优超分配
不优超分配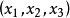 ,所以
,所以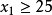 或者
或者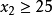 ;
;
分配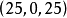 不优超分配
不优超分配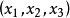 ,所以
,所以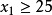 或者
或者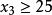 ;
;
分配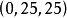 不优超分配
不优超分配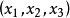 ,所以
,所以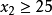 或者
或者 ;
;
因此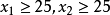 或者
或者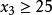 至少有两个必须同时成立,设是
至少有两个必须同时成立,设是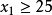 和
和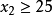 ,又因为
,又因为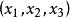 是一个分配,所以
是一个分配,所以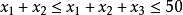 ,要这些都成立,只有
,要这些都成立,只有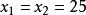 ,且
,且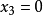 。这是稳定集中的一个分配,与
。这是稳定集中的一个分配,与 是稳定集外的分配矛盾,因此假设错误,则集合
是稳定集外的分配矛盾,因此假设错误,则集合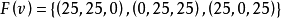 外的任一分配都至少被该集合内的一个分配优超。
外的任一分配都至少被该集合内的一个分配优超。
核心是一个唯一确定的集合,但稳定集不是,一个博弈可以有多个稳定集,并且稳定集也有可能是空集,卢卡斯(lucas)在1968年举出下面这个没有稳定集的合作博弈:
博弈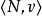 ,其中
,其中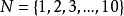 ,有特征函数:
,有特征函数:
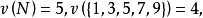
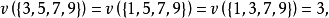
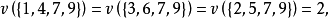
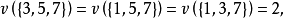
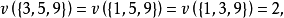
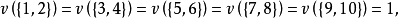 对于其他的联盟
对于其他的联盟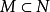 ,有
,有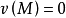 。卢卡斯证明了这个博弈没有稳定集2。
。卢卡斯证明了这个博弈没有稳定集2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国