[科普中国]-哈纳克引理

哈纳克引理是通过不等式描述区域上的正调和函数族的一个整体性质，是研究调和函数性质，特别是边界性质的重要工具。

简介哈纳克引理是通过不等式描述区域上的正调和函数族的一个整体性质。

若紧集K⊂D（D是Rn中的区域），则存在常数C=C(K,D)>0，使得不等式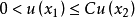对任何在D内调和的正值函数u>0和任意x1,x2∈K一致成立，这个性质称为哈纳克引理（或哈纳克不等式）。

应用哈纳克引理是研究调和函数性质，特别是边界性质的重要工具，该不等式有许多推广形式。1

调和函数调和函数是在某区域中满足拉普拉斯方程的函数。

通常对函数本身还附加一些光滑性条件，例如有连续的一阶和二阶偏导数。当自变量为n个（从而区域是n维的）时，则称它为n维调和函数。

对于高维的调和函数，也有与上述类似的最大、最小值原理，平均值公式以及相应的狄利克雷问题解的存在和惟一性定理。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所