[科普中国]-马尔可夫判决过程

简介

在概率论和统计学中，**马可夫决策过程（MDPs）**提供了一个数学架构模型，用于面对部分随机，部分可由决策者控制的状态下，如何进行决策，以俄罗斯数学家安德雷·马尔可夫的名字命名。在经由动态规划与强化学习以解决最佳化问题的研究领域中，马可夫判决过程是一个有用的工具。

马尔可夫过程在概率论和统计学方面皆有影响。一个通过不相关的自变量定义的随机过程，并（从数学上）体现出马尔可夫性质，以具有此性质为依据可推断出任何马尔可夫过程。实际应用中更为重要的是，使用具有马尔可夫性质这个假设来建立模型。在建模领域，具有马尔可夫性质的假设是向随机过程模型中引入统计相关性的同时，当分支增多时，允许相关性下降的少有几种简单的方式。

马尔可夫判决过程是指决策者周期地或连续地观察具有马尔可夫性的随机动态系统，序贯地作出决策。即根据每个时刻观察到的状态，从可用的行动集合中选用一个行动作出决策，系统下一步（未来）的状态是随机的，并且其状态转移概率具有马尔可夫性。决策者根据新观察到的状态，再作新的决策，依此反复地进行。马尔可夫性是指一个随机过程未来发展的概率规律与观察之前的历史无关的性质。马尔可夫性又可简单叙述为状态转移概率的无后效性。状态转移概率具有马尔可夫性的随机过程即为马尔可夫过程。马尔可夫判决过程又可看作随机对策的特殊情形，在这种随机对策中对策的一方是无意志的。马尔可夫判决过程还可作为马尔可夫型随机最优控制，其决策变量就是控制变量。

发展概况50年代，R.贝尔曼研究动态规划时和L.S.沙普利研究随机对策时已出现马尔可夫判决过程的基本思想。R.A.霍华德(1960)和D.布莱克韦尔(1962)等人的研究工作奠定了马尔可夫判决过程的理论基础。1965年，布莱克韦尔关于一般状态空间的研究和E.B.丁金关于非时齐（非时间平稳性）的研究，推动了这一理论的发展。1960年以来，马尔可夫判决过程理论得到迅速发展，应用领域不断扩大。凡是以马尔可夫过程作为数学模型的问题，只要能引入决策和效用结构，均可应用这种理论。

定义马尔可夫判决过程是一个五元组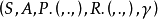 ，其中1，

1)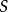 是一组有限的状态；

2)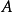 是一组有限的行为（或者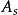， 是从状态可用的有限的一组行动 ）；

3)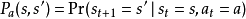 是行动的概率 在状态 在时间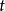 会导致状态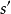 在时间 ；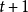

4)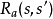 是从国家转型后得到的直接奖励（或期望的直接奖励）；

5)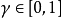 是折现系数子，代表未来奖励与现在奖励之间的重要差异。

（注：马尔可夫决策过程的理论并没有说明这一点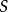 要么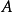 是有限的，但是下面的基本算法假设它们是有限的）。

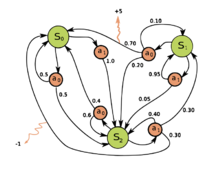
图1表示具有三个状态（绿色圆圈）和两个动作（橙色圆圈）的简单MDP的示例。

描述MDP的核心问题是为决策者找到一个“判决”：一个功能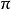 指：决策者什么时候会选择行动 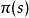。一旦马尔可夫决策过程以这种方式与政策相结合，就可以解决每个状态的行为，并且产生的组合行为就像一个马尔可夫链。

目标是选择一项判决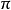 这将最大化随机奖励的一些累积函数，通常是在可能无限的时间范围内的期望折扣总和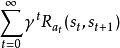： ，这里选择的地方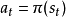。 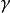是折扣因素和满足 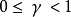。例如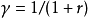， 当折扣率为r时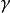， 通常接近1。

由于马尔可夫属性，这个特定问题的最优策略确实可以写成一个函数 只有，如上所述。

策略指标策略是提供给决策者在各个时刻选取行动的规则，记作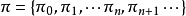 ，其中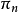 是时刻n选取行动的规则。从理论上来说，为了在大范围寻求最优策略 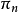，最好根据时刻 以前的历史，甚至是随机地选择最优策略。但为了便于应用，常采用既不依赖于历史、又不依赖于时间的策略，甚至可以采用确定性平稳策略。

衡量策略优劣的常用指标有折扣指标和平均指标。折扣指标是指长期折扣〔把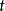 时刻的单位收益折合成0时刻的单位收益的 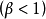倍〕期望总报酬；平均指标是指单位时间的平均期望报酬。

采用折扣指标的马尔可夫决策过程称为折扣模型。业已证明：若一个策略是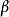 折扣最优的，则初始时刻的决策规则所构成的平稳策略对同一也是折扣最优的，而且它还可以分解为若干个确定性平稳策略，它们对同一β都是最优的，已有计算这种策略的算法。

采用平均指标的马尔可夫决策过程称为平均模型。已证明：当状态空间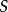 和行动集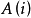 均为有限集时，对于平均指标存在最优的确定性平稳策略；当 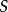和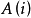 不是有限的情况,必须增加条件，才有最优的确定性平稳策略。计算这种策略的算法也已研制出来。

扩展1.约束马尔可夫判决过程约束马尔可夫决策过程（CMDPs）是马尔可夫决策过程（MDPs）的扩展。MDPs和CMDPs有三个基本的区别。

1）应用时一个动作而不是一个动作需要多个成本；

2）CMDP只能通过线性程序来解决，动态编程不起作用；

3）最终的判决取决于开始的状态。

CMDP有很多应用。它最近被用在机器人的运动规划场景中。

2.模糊马尔可夫判决过程（FMDPs）在MDPs中，最优策略是使未来奖励的概率加权总和最大化的策略。因此，最优策略由几个属于一组有限行为的动作组成。在模糊马尔可夫判决过程（FMDPs）中，首先，价值函数被计算为规则的MDPs（即具有有限的一组行动）；那么，这个策略是通过一个模糊推理系统来提取的2。换句话说，价值函数被用作模糊推理系统的输入，策略是模糊推理系统的输出。