排队过程是描述按一定规律等待服务和正在被服等的需求个数的随机过程。考虑“顾客”在随机时刻到达一服务系统,要求提供某种服务。如果顾客到达时有空余的“服务员”,则他可以马上得到所要的服务,否则他必须等待一段随机时间。每个顾客占用的服务时间也是随机变量。于是顾客在随机时刻到达,又在随机时刻离去。以Xt,t≥0表示时刻t时正在被服务和等待服务的顾客个数(队长),则{Xt,t≥0}是一个连续时间非负整值随机过程,称为“排队过程”,通常它是连续时间马尔可夫链;排队过程的性质取决于如下主要因素:1、服务规则:先来先服务或其他带某种优先规定的规则等。2、服务人个数:单服务员、多服务员,或者服务员相当多时可认为有无限多个服务员。3.顾客到达时间间隔的统计性质:例如是否相互独立,是否同分布;同服从哪种分布等(通常假定到达时间间隔独立同分布)。4.顾客占用服务时间的统计性质(也可讨论与上述到达时间间隔相类似的问题)。排队过程在系统科学,经营管理等领域有重要的应用1。
排队系统的组成和特征一般的排队系统都有三个基本组成部分:(1)输人过程;(2)排队规则;(3)服务机构。
下面分别说明各部分的特征2。
输人过程输人即指顾客到达排队系统,可能有下列各种不同情况,当然这些情况并不是彼此排斥的。
(1) 顾客总体(称为顾客源)的组成可能是有限的,也可能是无限的。犹如上游河水流人水库,可以认为总体是无限的,工厂内停机待修的机器显然是有限的总体。
(2) 顾客到来的方式可能是一个一个的,也可能是成批的。例如,到餐厅就餐就有单个到来的顾客和受邀请来参加宴会的成批顾客。
(3) 顾客相继到达的间隔时间可以是确定型的,也可以是随机型的。例如,在自动装配线上装配的各部件就必须按确定的时间间隔到达装配点,定期运行的班车、班轮、班级的到达也都是确定型的。但一般到商店购物的顾客、到医院诊病的病人、通过路口的车辆等,他们(或它们)的到达都是随机型的。对于随机型的情形,要知道单位时间内的顾客到达数或相继到达的间隔时间的概率分布。
(4) 顾客的到达可以是相互独立的,也就是说,以前的到达情况对以后顾客的到来没有影响,否则就是有关联的。例如,工厂内的机器在一个短的时间区间内出现停机(顾客到达)的概率就受已经待修或被修理的机器数目的影响。
(5) 输人过程可以是平稳的,或是对时间齐次的,是指描述相继到达的时间间隔分布和所含参数(如期望值,方差等)都是与时间无关的,否则成为非平稳的。非平稳情形的数学处理很困难。
排队规则(1) 顾客到达时,如所有服务台都正被占用,在这种情形下顾客可以随即离去,也可以排队等候。随即离去的称为即时制或称损失制,因为这将失掉许多顾客;排队等候的称为等待制。普通市内电话的呼唤属于前者,而登记市外长途电话的呼唤属于后者。对于等待制,为顾客进行服务的次序可以采用下列各种规则:先到先服务、后到先服务、随机服务、有优先权的服务等。
先到先服务,即按到达次序接受服务,这是最通常的情形。
后到先服务,如乘用电梯的顾客常是后人先出的。仓库中存放的厚钢板也是如此。在情报系统中,最后到达的信息往往是最有价值的,因而常采用后到先服务(指被采用)的规则。
随机服务,指服务员从等待的顾客中随机选取其一进行服务,而不管到达的先后,如电话交换台接通呼唤的电话就是如此。
有优先权的服务,如医院对于病情严重的患者将给予优先治疗。
(2) 从占有的空间来看,队列可以排在具体的处所(如售票处、候诊室等),也可以是抽象的(如向电话交换台要求通话的呼唤)。由于空间的限制或其他原因,有的系统要规定容量(即允许进人排队系统的顾客数)的最大限制;有的没有这种限制(即认为容量可以是无限的)。
(3) 从队列的数目看,可以是单列,也可以是多列。在多列的情形,各列间的顾客有的可以互相转移,有的不能(如用绳子或栏杆隔开)。有的排队顾客因等候时间过长而中途退出,有的不能退出(如高速公路上的汽车流),必须坚持到被服务为止。
服务机构从机构形式和工作情况来看有以下五种情况。
(1) 服务机构可以没有服务员,也可以有一个或多个服务员(服务台、通道、窗口等)。例如,在敞架售书的书店,顾客选书时就没有服务员,但交款时可能有多个服务员。
(2) 在有多个服务台的情形中,它们可以是平行排列(并列)的,可以是前后排列(串列)的,也可以是混合的。
(3) 服务方式可以对单个顾客进行,也可以对成批顾客进行,公共汽车对在站台等候的顾客就属于成批进行服务。
(4) 和输人过程一样,服务时间也分确定型的和随机型的。自动冲洗汽车的装置对每辆汽车冲洗(服务)的时间就是确定型,但大多数情形的服务时间是随机型的。对于随机型的服务时间,需要知道概率分布。
如果输人过程,即相继到达的间隔时间,和服务时间都是确定型,那么问题就太简单了,因此,在排队论中所讨论的是二者至少有一个是随机型的情形2。
排队模型的概述排队系统的主要数量指标研究排队系统的主要目的是通过了解系统运行的状况,对系统进行调整和控制,使系统处于最优运行状态。因此,首先需要弄清系统的运行状况。描述一个排队系统运行状况的主要数量指标有:
队长和队列长(排队长)。队长是指系统中的顾客数(排队等待的顾客与正在接受服务的顾客数之和);队列长是指系统中正在排队等待服务的顾客数。队长和队列长般都是随机变量。队长的分布是顾客和服务员都关心的;特别是对系统设计人员来说,如果能知道队长的分布,就能确定队长超过某个数的概率,从而确定合理的等待空间。
等待时间和逗留时间。从顾客到达时刻起到开始接受服务止的这段时间称为等待时间。等待时间是个随机变量,也是顾客最关心的指标,因为顾客通常是希望等待时间越短越好。从顾客到达时刻起到他接受服务止的这段时间称为逗留时间,也是随机变量,顾客同样非常关心。
忙期和闲期。忙期是指从顾客到达空闲着的服务机构起,到服务机构再次成为空闲止的这段时间,即服务机构连续忙的时间。这是个随机变量,是服务员最为关心的指标,因为它关系到服务员的服务强度。与忙期相对的是闲期,即服务机构连续保持空闲的时间。在排队系统中,忙期和闲期是交替出现的。
除了上述几个基本数量指标外,还会用到其他一些重要指标。例如,在损失制或系统容量有限的情况下,由于顾客被拒绝,而使服务系统受到损失的顾客损失率及服务强度等,也都是十分重要的指标2。
排队系统的符号表示D.G.Kendall 于1953年提出一个分类方法,按照上述各部分的特征中最主要的、影响最大的三个分类:(1)相继顾客到达间隔时间的分布;(2)服务时间的分布;(3)服务台个数。
按照这三个特征分类,并用一定符号表示,称为Kendall****记号。这仅对并列的服务台(如果服务台多于1个的话)的情形,用的符号形式为
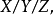 其中X处填写表示相继到达间隔时间的分布,Y 处填写表示服务时间的分布,Z处填写并列的服务台的数目。
其中X处填写表示相继到达间隔时间的分布,Y 处填写表示服务时间的分布,Z处填写并列的服务台的数目。
表示相继到达间隔时间和服务时间的各种分布的符号如下:
 ——负指数分布(M是Markov的字头,因为负指数分布具有无记忆性,即Markov性);
——负指数分布(M是Markov的字头,因为负指数分布具有无记忆性,即Markov性);
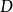 —— 确定型;
—— 确定型;
 —— k阶爱尔朗(Erlang)分布;
—— k阶爱尔朗(Erlang)分布;
 —— 一般相互独立(general independent)的时间间隔的分布;
—— 一般相互独立(general independent)的时间间隔的分布;
 ——一般服务时间的分布。
——一般服务时间的分布。
例如, 表示相继到达间隔时间为负指数分布、服务时间为负指数分布、单服务台的模型;
表示相继到达间隔时间为负指数分布、服务时间为负指数分布、单服务台的模型; 表示确定的到达间隔、服务时间为负指数分布、C个平行服务台(但顾客是一队)的模型。
表示确定的到达间隔、服务时间为负指数分布、C个平行服务台(但顾客是一队)的模型。
1971年,一次关于排队论符号标准化会议,将Kendall 符号扩充为
 形式,其中前项意义不变,而A处填写系统容量限制N,B处填写顾客源数目m,C处填写服务规则,如先到先服务FCFS、后到先服务LCFS等。
形式,其中前项意义不变,而A处填写系统容量限制N,B处填写顾客源数目m,C处填写服务规则,如先到先服务FCFS、后到先服务LCFS等。
同时约定,如略去后三项,即指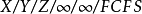 的情形2。
的情形2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国