平稳点过程(stationary point process)是一种随机点过程,在许多文献中是指具有平稳增量的随机点过程(等价地说,计数过程){N(t),t≥0},即对任意实数t>s≥0和h>0,过程在区间(s,t]和(s+h,t+h]中的点数(或者说,增量Ns,t=N(t)-N(s)和Ns+h,t+h=N(t+h)-N(s+h))有相同的分布。齐次泊松过程和平衡更新过程都是平稳点过程的特例1。
基本介绍具有平稳增量的计数过程 称为**平稳点过程。**平衡更新过程是平稳点过程的一个例子。
称为**平稳点过程。**平衡更新过程是平稳点过程的一个例子。
应当指出,有些文献把这一术语用于对任意有限多个区间,其增量有平稳联合分布的点过程。即对任意整数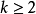 和实数
和实数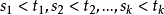 和
和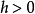 ,增量
,增量
 和
和
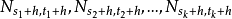 有相同的k维联合分布。这时,为了把前面提到的具有平稳区间分布的点过程和这种具有较强的平稳性要求的点过程区别开来,常常把前者称为粗平稳点过程1。
有相同的k维联合分布。这时,为了把前面提到的具有平稳区间分布的点过程和这种具有较强的平稳性要求的点过程区别开来,常常把前者称为粗平稳点过程1。
相关定理及证明定理1 除了对一切 有
有 的平凡情形以外,对任意平稳点过程有
的平凡情形以外,对任意平稳点过程有
 其中并不排除
其中并不排除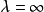 。
。
证明: 令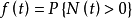 且注意到
且注意到 取非负值,且非减,又
取非负值,且非减,又
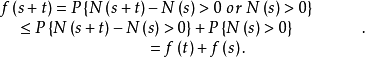 因此
因此
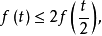 而由归纳法,对一切
而由归纳法,对一切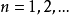 有
有
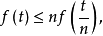 于是,令a使
于是,令a使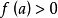 ,对一切
,对一切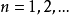 有
有
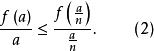 现在定义,由(2)我们得
现在定义,由(2)我们得
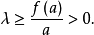 为了证明
为了证明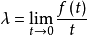 ,我们考虑两种情形。首先,假设
,我们考虑两种情形。首先,假设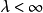 ,此时,固定
,此时,固定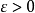 ,取
,取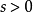 使
使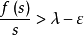 。现在对
。现在对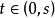 存在一个整数n使
存在一个整数n使
 由
由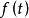 的单调性和式(2)可知,对这个区间中的一切t有
的单调性和式(2)可知,对这个区间中的一切t有
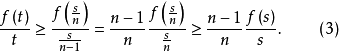 因此
因此
 由于
由于 是任意的,且当
是任意的,且当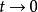 时
时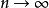 ,由此推出
,由此推出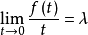 。
。
现在假定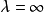 ,此时,固定任意很大的A>0,取s使
,此时,固定任意很大的A>0,取s使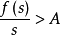 ,则由式(3)推出对一切
,则由式(3)推出对一切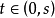 有
有
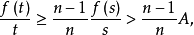 它蕴含
它蕴含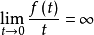 ,这就完成了证明2。
,这就完成了证明2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国