[科普中国]-更新过程

定义

定义一

在数学上更新过程可简单地定义为相邻两个点事件(即更新)的间距是相互独立同分布(但从原点到第一次更新的间距T1可以有不同分布)的计数过程.根据T1的分布情形更新过程又分为普通更新过程,延迟更新过程和平衡更新过程三类.更新过程也可用过程的事件间距序列{Tn,n≥1}给定,这时N(t)和Tn有如下关系∶N(t)=sup{n:Sn≤t}和Sn=inf{t:N(t)=n},其中

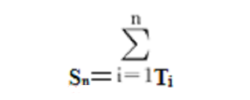
是第n次更新时间(n≥1,再定义S0=0).对于普通更新过程,Sn是n个相互独立同分布的非负随机变量之和,因此在数学上更新过程也可以看做是一类特殊的独立随机变量和.1

更新过程是Poisson过程的一种推广，其中事件发生的时间间隔是独立同分布的随机变量，分布函数为F2．

定义二

在故障报修方面的定义：

如果假设故障间隔时问Xi=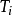 一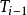 ( 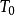=0)为来自某一分布的独立同分布样本，则随机过程Xi，i=1，2，…即为更新过程。其中，当故障间隔时间服从指数分布时，这一更新过程即为指数更新过程；当故障间隔时间服从Gamma分布时，这一更新过程即为Gamma更新过程。更新过程具有无记忆性，也就是说，对于一个更新过程，不管系统是全新的还是被修复了100次，下一次故障的实际都具有相同的分布，即更新过程描述了“修旧如新”维修效果。然而，需要注意的是，更新过程模型无法模拟通常在可修复系统中观测到的可靠性增长或可靠性衰减。对于更新过程模型，一个有用的指标是平均故障间隔时间(MTBF)，即故障间隔时间分布的均值．记为E(X)3。

举例为了用一个简单的比喻来讨论更新过程，考虑有一个非常勤快的门卫管理电灯，当灯泡烧坏时，就立即更换．令ti表示第i个灯泡的寿命．假设灯泡都是从同一厂家购买的，从而我们设2

P(ti≤t)=F(t)

其中F是分布函数，F(0)=P(ti≤0)=0．

如果在时刻0从一个新灯泡(编号为1)开始，一旦灯泡烧坏，就立即更换新的灯泡，那么Tn=t1+…+tn表示第n个灯泡烧坏的时刻，

N(t)=max{n：Tn≤t}

表示到时刻t为止已更换的灯泡数，那么过程的路径和Poisson过程的相应结果是类似的，如果更新理论仅仅和更换灯泡有关的话，那它就不是一个非常有用的研究对象了．我们关注这个系统的原因是它抓住了很多不同情形的本质．我们已经看到过的例子如下．2

1.Markov链 令Xn表示一个Markov链，设Xn=x．Tn表示过程第n次返回到x的时刻．根据强Markov性可知tn=Tn一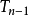 是相互独立的，因此Tn是一个更新过程．

2.维修机器 考虑一台机器而不是一个灯泡，机器发生故障前正常工作的时间为si,发生故障后需要花费ui时间才能修理好机器．令ti=si+ui，表示机器发生故障并维修好的第i个循环的时问长度．如果我们假定维修机器可使得它处于“宛如新机器”的状态，那么ti是独立同分布的，因此可以得到一个更新过程．

3.计数过程 在诸如医学成像的应用中会出现下面的情形：粒子按照速率为λ的Poisson过程到达计数器．当一个粒子到达计数器时，如果计数器是空闲的，则进行计数．并锁定计数器τ时长．当粒子在计数器处于锁定期间到达时不产生任何效果．如果假定计数器从未锁定的状态开始，则计数器第n次变为未锁定状态的时刻Tn可形成一个更新过程．这是前面例子的一个特殊情形：ui=τ，si=速率为λ的指数随机变量．此外，更新过程在排队论中有很多应用。2

重要结论更新过程的第一个重要结论是如下的大数定律．2

定理1 令μ=E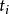 表示平均间隔时间．如果P( 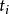>0)>0，那么以概率1有2

当t→∞时，N(t)/t→1/μ

用文字叙述，是说如果灯泡平均使用了μ年时间，那么在t年中我们将用坏大约t/μ个灯泡．因为在Poisson过程中时间间隔服从均值为1/λ的指数分布，根据定理1可知，如果N(t)表示Poisson过程中在时刻t之前的总到达数，那么

当t→∞时，N(t)/t→λ

定理1的证明 我们利用下面的强大数定律．

定理2(强大数定律) 令x1，x2，x3，…独立同分布，Exi=μ，Sn=x1+…+xn,则以概率1有2

当n→∞时，Sn/n→μ

取xi=ti，则有Sn==Tn因此定理2意味着当n→∞时，Tn/n以概率1收敛于μ.

根据定义，

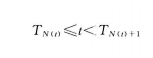
除以N(t)，有

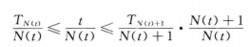
根据强大数定律，左边和有边都收敛于μ．据此即可得t/N(t)→μ，从而N(t)/t→1/μ.