[科普中国]-复合泊松过程

基本概念

复合泊松过程(compound Poisson process)一类随机过程。是由对泊松过程的每一点赋予一独立同分布的随机变量而得的随机过程.对于随机过程{X(t)，t≥0}如果对任意t≥0，它能表为

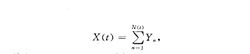
其中{N(t)，t≥0}是一泊松过程，而{Y,n=1,2,... }是一族独立同分布的随机变量，并且过程{N(t)，t≥0}与序列{Yn}是相互独立的，则将它称为复合泊松过程。

1 复合泊松过程可以看做是在泊松过程的点附上标值(用随机变量Yn表示)而得，因而是一类特殊的标值点过程.另一方面，复合泊松过程也可看做是一类特殊的滤过泊松过程，这时响应函数ω(t，τn，un)=Yn(参见“标值点过程”和“滤过泊松过程”)。

计数过程泊松过程是计数过程中最重要的类型之一，所以要了解泊松过程和复合泊松过程就要先了解计数过程，下文为计数过程的介绍。

称随机过程{N(t), t ≥0}为计数过程，若N(t)表示到时刻，为止已发生的“事件A”的总数，且N(t)满足下列条件:

(1)N(t)≥0;
(2 ) N(t)取正整数值;
(3)若s