[科普中国]-可分对策

可分对策(separable game)是一类特殊的无限对策。称这样的策略分别是局中人Ⅰ和Ⅱ在可分对策中的最优策略。称这样的值E(r*，s*)为可分对策的最优值。

概念可分对策(separable game)是一类特殊的无限对策。其赢得函数(亦称可分函数)为：

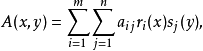式中aij是常数，ri(x)和sj(y)是连续函数(i=1，2，…，m;j=1，2，…，n).当局中人Ⅰ期望支付的最小值等于局中人Ⅱ期望支付的最大值时，即：

(式中r*=(r*1，r*2，…，r*m)∈R，s*=(s*1，s*2，…，s*n)∈S)时，则称这样的策略分别是局中人Ⅰ和Ⅱ在可分对策中的最优策略。称这样的值E(r*，s*)为可分对策的最优值。1

对策论运筹学的一个分支，它通过对竞争活动或斗争局势的模型(即对策)，加以描述和研究，为竞争或斗争的各方，提供如何作出收益最大或损耗最小之决策的一种数学分析方法。它最初讨论的是象棋、扑克和桥牌等竞争性娱乐活动的对策。因此，又称为博奕论。

据《史记》记载：战国时，齐王与田忌赛马，双方都有上、中、下三个等级的马各一匹，每次双方出一匹马参加比赛，共进行三次。虽然田忌的马都比齐王同一等级的马差，但是由于田忌的谋士孙膑(著名军事家)为他设计了如下的对策：用下马对齐王的上马;用上马对齐王的中马；用中马对齐王的下马，田忌反而以2：1取胜。这就是使用对策论思想一个最早的例子。

1943年，冯·诺伊曼与摩根斯顿(O.Morgenstern，美籍德国人，1902—1977)对竞争性经济活动进行了系统的研究，对策论开始成为一门学科。由于电子计算机的出现，它得到了迅速的发展。

在对策论中，研究对立的双方在竞争性活动中，各自为制胜对方所取最优策略的存在与求法等问题。例如，对于敌我双方的潜艇与反潜艇飞机，都存在各自应采取怎样的航线，使得尽可能保存自己，又能尽量消灭对方的对策问题。

对策论所研究的，可以是由两方参加的，也可以是由多方参加的竞争活动；而且参加者不一定是完全对立的，还允许他们结成某种联盟;活动的结局，也可能要参加者通过多次决策才能决定。对控制系统来说，竞争的双方都不是人，其中一方是客观环境，另一方是控制系统本身。因此，对策论不仅在军事(战术)上，而且在人与自然界作斗争，以及经济学、管理科学以及外交谈判、贸易谈判中，甚至在社会科学、行为科学(例如罪犯侦缉问题)等各个方面，都得到了应用。

对策问题三要素对策论的三个基本概念。指对策问题中的局中人、策略和对策的得失。

局中人是指在一局对策(竞争或斗争)中，有决策权的参加者.局中人可以是个人，也可是集团。局中人一般用记号Ⅰ，Ⅱ，…表示，而用字母Ⅰ表示所有局中人构成的集合。只有两个局中人的对策，称为两人对策.多于两个局中人的对策，称为多人对策。策略是局中人在对策中采用的一个可行的自始至终通盘筹划的行动方案。局中人策略的全体称为策略集合，它可以是有限集，也可以是无限集。局中人在一局对策结束时的得失称为对策的得失。一局对策结束时，每个局中人的“得失”是全体局中人所取定的一组策略的函数，称为支付函数，亦称赢得函数.称赢得函数为连续函数的对策为连续对策。从每个局中人的策略集中各取一个策略组成的策略组，称为对策的一个局势。对策的得失是局势的函数。2

策略策略是动态规划的基本概念之一。指由每一阶段的决策ui(xi)(i=1，2，…，n)组成的决策函数序列，记为：

P1，n(x1)={u1(x1)，u2(x2)，…，un(xn)}。

由第k阶段开始到终点为止的决策函数序列称为子策略，记为：

Pk，n(xk)={uk(xk)，uk+1(xk+1)，…，un(xn)}。

由第k阶段开始到终点的过程，称为原过程的后部子过程或称为k子过程。

动态规划动态规划是优化理论和运筹学的一 个重要分支，它是解决多阶段决策过程的一种优化 方法。它的理论根据是L.R.Bellman等人提出的 “最优化原理”。动态规划问题没有标准的数学构 成，只有求解问题的一般性六个步骤：

(1)将问题恰当地划分若干阶段；

(2)正确地确定每一阶段有若干个可能状态；

(3)每一阶段上的决策效益是从一种状态转移到下一阶段某个状态时对目标函数所作的贡献；

(4) 写出状态转移方程；

(5)确定各阶段各种决策的直接指标： 列出计算各阶段最优策略指标的递推方法；

(6)求解过程从寻求最后阶段的每种状态下的最优决策开始，按与实际过程相反的方向，向最初阶段推移。

近年来，动态规划在工程技术、经济、工业生产及军事等部门都有广泛应用，并获得显著成就。

动态规划问题可根据决策过程是有限阶段或是无限阶段而分类；还可根据状态变量划分为连续状态变量问题或离散状态变量问题；以及是否含有随机性参量划分为随机性和确定性两类等等。3

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学