凸对策(convex game)是一类有特殊赢得函数的对策,如果对于局中人Ⅰ的任意纯策略x∈X,赢得函数A(x,y)是y的一个凸函数,称此对策G为凸对策1。
基本概念设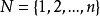 为局中人集,
为局中人集,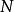 上对策全体仍记为
上对策全体仍记为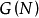 或
或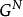 ,
,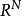 (或
(或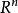 )为
)为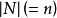 维欧几里德空间。
维欧几里德空间。
任给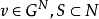 ,定义
,定义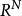 中超平面
中超平面
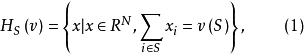 在不引起混淆的前提下,记
在不引起混淆的前提下,记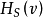 为
为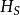 。
。
设 为
为 人对策。如果对
人对策。如果对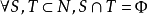 ,均有
,均有
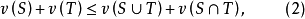 则称
则称 为凸对策(convexgame)。如果当
为凸对策(convexgame)。如果当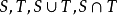 均不相同时,(2)中严格不等式成立,则称
均不相同时,(2)中严格不等式成立,则称 为严格凸对策(strictly convex game)2。
为严格凸对策(strictly convex game)2。
凸对策的性质下面介绍凸对策的一些性质。
性质1对固定的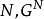 上所有凸对策全体形成凸锥(convex cone)2。
上所有凸对策全体形成凸锥(convex cone)2。
性质2 设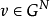 ,则
,则 是凸对策的充要条件为:
是凸对策的充要条件为:
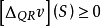 对任意
对任意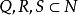 成立。
成立。
性质2表明凸对策具有与凸函数类似性质,因为当函数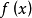 满足
满足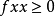 时,则,
时,则,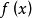 是凸的,因此,凸对策充要条件是二阶差分大于或等于零。这也是凸对策名称的由来。
是凸的,因此,凸对策充要条件是二阶差分大于或等于零。这也是凸对策名称的由来。
性质3凸对策在策略等价意义下不变,即若 是凸对策,而
是凸对策,而 和
和 策略等价,则
策略等价,则 也是凸对策。
也是凸对策。
性质4 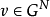 ,则下列条件等价
,则下列条件等价
(i)  是凸对策;
是凸对策;
(ii)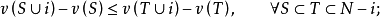
(iii)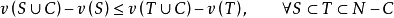 。
。
给定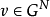 ,由于核心C是凸多面体,为了刻画凸对策解的结构,我们引进一些概念。
,由于核心C是凸多面体,为了刻画凸对策解的结构,我们引进一些概念。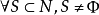 ,记
,记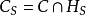 ,显然
,显然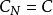 ,为方便起见,记
,为方便起见,记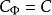 。
。
定义1 给定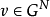 ,如果对
,如果对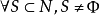 ,则称核心构形(core configuration)
,则称核心构形(core configuration)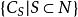 为完全构形(complete configuration)。
为完全构形(complete configuration)。
定义2 给定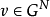 ,如果核心构形
,如果核心构形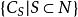 满足
满足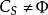 ,且
,且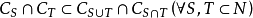 成立,则称
成立,则称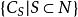 为有规则(regular)构形。
为有规则(regular)构形。
性质5 设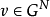 为凸对策,则
为凸对策,则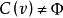 。
。
推论设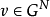 ,则
,则 是凸对策的充要条件是对
是凸对策的充要条件是对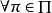 ,有
,有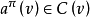 。
。
引理7设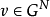 ,
,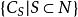 为有规则构形,则对任何递增序列
为有规则构形,则对任何递增序列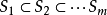 ,
,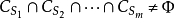 。特别地,当
。特别地,当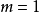 ,有规则构形为完全构形。
,有规则构形为完全构形。
性质6 给定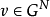 ,
, 是凸对策的充要条件是核心构形
是凸对策的充要条件是核心构形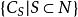 是有规则构形。
是有规则构形。
性质7设 是凸对策,则核心
是凸对策,则核心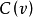 是唯一的稳定集。
是唯一的稳定集。
下面将转向凸对策的核的研究。如果 是0-单调对策,则
是0-单调对策,则 的核
的核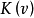 与准核
与准核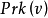 相等,即
相等,即
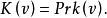
性质7设v是凸对策,则
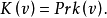
性质8设 是凸对策,于是
是凸对策,于是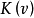 只包含一个点。
只包含一个点。
因此,如果 是一凸对策,核、准核以及核子三者都是重合的,可用求字典序的方法来求出凸对策的核2。
是一凸对策,核、准核以及核子三者都是重合的,可用求字典序的方法来求出凸对策的核2。
本词条内容贡献者为:
武伟 - 高级工程师 - 天津直升机有限责任公司




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国