[科普中国]-传递函数矩阵

简单系统的传递函数矩阵

一控制系统的状态空间表达式如下

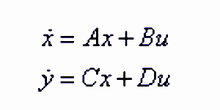
简写为（A、B、C、D）}

式中x为n维状态向量；y为q维输出向量；u为p维输入向量；A为n×n维系统矩阵；B为n×p维输入矩阵；C为q×n维输出矩阵；D为q×p维前馈矩阵。1

假定系统初始状态为0，其拉普拉斯变换后的表达式为

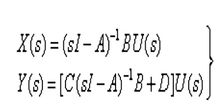
式中(sI-A)-1B称为输入-状态传递函数矩阵；C(sI-A)-1B十D称为输入-输出传递函数矩阵，简称传递函数矩阵，它是一个q×p维矩阵，它的每一个元素反映了某个输入变量对某个输出变量的传递函数。一个控制系统的传递函数矩阵是一定的，不因坐标变换而变化。

复杂系统的传递函数矩阵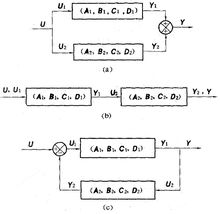实际的控制系统往往由多个子系统组合而成，或并联，或串联，或形成反馈连接，或是它们的组合。组合系统的输入-输出传递函数矩阵可由各子系统的输入-输出传递函数矩阵组合而成。下图为基本组合系统的框图。图(a)示出两个子系统的并联，其输入-输出传递函数矩阵W(s)=W1(s)+W2(s)，式中W1(s)，W2(s)分别为子系统(A1，B1，C1，D1)和(A2，B2，C2，D2)的输入-输出传递函数矩阵。图(b)示出两个子系统的串联，其输入-输出传递函数矩阵为W(s)=W2(s)W1(s)。图(c)示出由反馈子系统构成的组合系统，其输入-输出传递函数矩阵为W (s)=W1 (s) [I+W2(s)W1(s)]-1或W(s)=[I+W1(s)W2(s)]-1W1(s)。

当控制系统维数不高时，可直接由adj(sI-A)/|sI-A|求得(sI-A)-1，其中|sI-A|为(sI-A)矩阵的行列式，adj(sI-A)为(sI-A)矩阵的伴随矩阵。当控制系统维数较高时，这样的方法计算过程太复杂，可用其他更简便的方法。

对许多实际系统而言，D矩阵往往是0矩阵，|sI-A|的根为系统的极点，Cadj (sI-A)B中各元素多项式的根为系统的零点。存在零点、极点相消的情况下，传递函数矩阵就不能完全描述系统的运动规律及性能，只能反映系统完全可控且完全可观测部分的情况。 2