[科普中国]-因子覆盖图

因子覆盖图(factor covered graph)是一类特殊的图。指每一条边都在同一种因子之中的图。若图中的每一条边都包含在某个1因子之中，则称G为1因子覆盖图。G的节点v称为完全覆盖点，若v的每条与之关联的边均有G的一个1因子包含它。1

概念因子覆盖图(factor covered graph)是一类特殊的图。指每一条边都在同一种因子之中的图。若图中的每一条边都包含在某个1因子之中，则称G为1因子覆盖图。G的节点v称为完全覆盖点，若v的每条与之关联的边均有G的一个1因子包含它。

图图的定义是随着图论的发展而逐步推广的。最初图被直观描述为：所谓图就是一些点和连接点的边所构成的图形。以后将此描述严格定义为：2

定义1 给定非空集合V，E是V的若干二元子集做成的集合，则G=(V，E)称为一个图。V中每一元素叫做图G的结点，E中每一元素(即V中某个二元子集) {a，b}称为图G中连接结点a和b的边，结点a和b称为邻接的。

这样定义的图现在称为简单图，因为在这些图中每两个点最多只能有一条边连接，且任何结点到自身没有边连接。随着生产实践的发展，更广泛的一类图被引入。

定义2 V为一个非空集合，E为任意集合，ᵠ为E到V中无序偶对集合上的函数，则G=(V，E，ᵠ)称为一个图。V中的元素称为图G的结点。对任何e∈E，若ᵠ(e)={a，b}，则e称为图G中连结a，b两点的边。

显然，这样定义的图两结点间可以有不止一条边，且结点到自身也可以有边连接。若两结点间有不止一条边连接，则这些边称为平行边。对应于简单图，具有平行边的图有时也称为多重图。

后来，图的定义又得到进一步的推广，引入所谓方向的概念，即给每一条边赋予一个方向。

定义3 V为非空集合，E为任意集合，ᵠ为E到V×V的函数，则G=(V，E，ᵠ)称为一个图。对任意e∈E，若ᵠ(e)= (a，b)，则e称为图G中从a到b的有向边，a称为e的始点，b称为e的终点。

对应于上面所定义的没有方向的图，这里所定义的图有时又称为有向图，而将原来的图称为无向图。

随着图论的发展，由实际问题抽象出来的图中结点和边上往往都带有信息，因此又引入赋数图的概念。所谓赋数图是一个三重组 (V，E，g)或四重组(V，E，f，g)，其中V是结点集合，E是边的集合，f是定义在V上的函数，g是定义在E上的函数。对任何υ∈V，e∈E，f(υ)，g(e)分别称为点υ和边e上的数。

子图图论的基本概念之一。指节点集和边集分别是某一图的节点集的子集和边集的子集的图。若这个节点子集或边子集是真子集，则称这个子图为真子图。若图G的每一个节点也是它的子图H的节点，则称H是G的支撑子图。设S是V(G)的子集，以S为节点集，以G的所有那些两端点都在S内的边组成边集，所得到的G的子图称为S在G中的导出子图，或更确切地，节点导出子图。设B是E(G)的子集，由G的所有与B内至少有一条边关联的节点组成节点集，以B为边集，所得到的G的子图称为B在G中的边导出子图。对于某种性质P，若一个图的具有P的子图不是任何具有P的子图的真子图，则称它为具有P的极大子图。在所有极大子图中，边数最多的那个称为最大子图。3

部图一类特殊的图。即一个图的节点集可分成若干个子集，使得每一条边的两端点不在同一子集内。若一个图的节点集能分成k个两两不交的非空子集，使得这个图的每一条边的两端点不在同一个子集内，则称这个图为k部图。若k=2，则称这种k部图为二部图；若k=3，则称这种k部图为三部图。若在一个k部图中，任一节点与其他部的所有节点都相邻，则称它为完全k部图。

图论近年来比较活跃的数学分支之一。图论是研究各种图的性质和特征的一门理论，主要包括图与子图、图的连通性、可平面性、正则图、树、着色问题、图的矩阵以及网络等内容。图论的发展已有200多年的历史。早在18世纪中叶就已出现有关图的文字记载。这时的图论尚处于萌芽阶段，多数问题是围绕着游戏而产生的，最有代表性的是著名的哥尼斯堡七桥问题(相当于我国的一笔画问题)。19世纪中叶到20世纪中叶，图论问题大量出现，诸如哈密尔顿“绕行世界”问题，关于地图着色的四色问题以及与之有关联的图的可平面性等等。在这个阶段，也出现了以图为工具去解决其他领域中一些问题的成果，例如，凯莱把图论应用到有机化学中关于同分异构物的计数问题，克希霍夫应用树研究电网络的分析问题等等。20世纪中叶以后，由于生产管理、军事、交通运输、计算机网络等方面提出的实际问题的需要，特别是许多离散性问题的出现，以及由于有了大型超高速计算机，而使大规模问题的求解成为可能，图论及其应用的研究得到了飞速发展。这个阶段的开创性工作是以福特和福克逊建立的网络流理论为代表的。图论和线性规划、动态规划等优化理论和方法的相互渗透，促进了组合最优化理论和算法的研究以及图论对实际问题的应用，与此同时也丰富了图论的内容，使图论的发展更加充满活力。

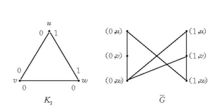
覆盖图覆盖图是一类重要的图。它是从一个图派生的图。对图G的每一条边(u，v)给出两个侧[u，v)(即含u而不含v)和[v，u)(即含v而不含u)。记S(G)为G的所有边的两侧组成的集合。对于群Γ，G上的一个Γ链是从S(G)到Γ的一个函数φ，对G的所有侧[u，v)，满足：φ[u，v)=(φ[v，u))-1。4

对给定的图G的Γ链φ，G的覆盖图G~：其顶点集为Γ×V(G)；两顶点(a，v)，(b，u)相邻当且仅当[v，u)∈S(G)且b=aφ[v，u)。例如，Γ={0，1}，G=K3，即3阶的完全图。G~如下图所示。在K3中边旁之两数字给出φ的值。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学