[科普中国]-边覆盖

定义

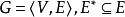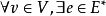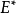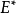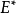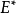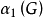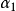设图，若，使得v与e相关联，则称e覆盖v，并称为边覆盖集，或简称边覆盖。设为边覆盖，若的任何真子集都不是边覆盖，则称是极小边覆盖。边数最少的边覆盖集称为最****小边覆盖，其所含边的个数称为边覆盖数，记作，或简记为。2

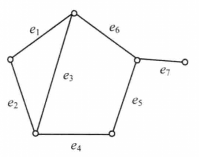
在图1(a)中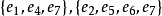，都是极小边覆盖，其中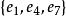是最小边覆盖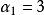，。(b)中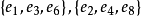都是极小边覆盖，。

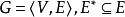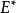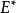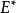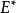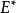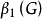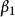相关概念设，若中任何两条边均不相邻，则称为G中边独立集，也称为G中的匹配。若在中再加任意一条边后，所得集合都不是匹配，则称为极大匹配。边数最多的匹配称为最大匹配，其边数称为独立数或匹配数，记作或简记为。2

在图1(a)中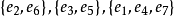，都是极大匹配，其中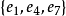是最大匹配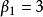，。(b)中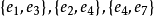都是极大匹配，同时也都是最大匹配，。

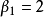常用M表示匹配，极大匹配，最大匹配等。

设M为图G中一个匹配。

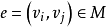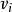(1)设，则称与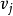被M所匹配。

(2)对于任意的，若存在边e∈M，使e与v关联，则称v为M-饱****和点．否则称v为M-非饱和点。

(3)若G中每个顶点都是M-饱和点，则称M为G中的完美匹配。

(4)称G中在M和(E(G)-M)中交替取边的路径为M的交错路径，起点和终点都是M-非饱和点的交错路径称为可增广的交错路径。称G中在M和(E(G)-M)中交替取边的圈为交错圈。

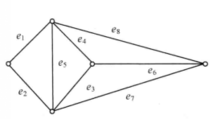
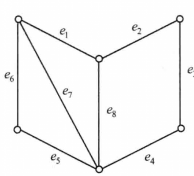
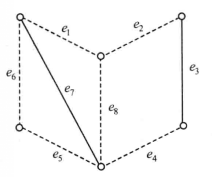
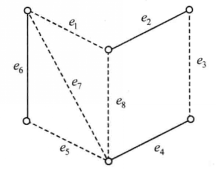
在图2(a)中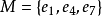，为完美匹配，(b)中不可能有完美匹配，因而对任何匹配都存在着M-非饱和点。

另外，在图1(a)中的最大匹配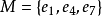，它也是图中的最小边覆盖。而在(b)中，任给一个最大匹配，比如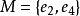．则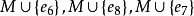，都是图中的最小边覆盖。反之，给定(b)中的一个最小边覆盖，比如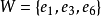，从中移去一条相邻的边，则都是图中的最大匹配，这种由最大匹配通过增加关联非饱和点的边产生最小边覆盖，和由最小边覆盖通过移去相邻的一条边产生最大匹配的方法具有普遍性。2

相关定理定理1设n阶图G中无孤立点。

(1)设M为G中的一个最大匹配，对于G中每个M-非饱和点均取一条与其关联的边，组成边集N，则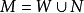为G中最小边覆盖。

(2)设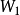为G中的一个最小边覆盖，若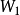中存在相邻的边就移去其中的一条，设移去的边集为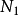，则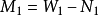为G中一个最大匹配。

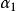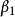(3)G中边覆盖数与匹配数满足：。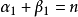

推论1设G是n阶无孤立点的图。M为G中的匹配，W是G中的边覆盖，则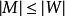。等号成立时,M为G中完美匹配。2

定理2M为G中的最大匹配当且仅当G中不含M可增广的交错路径。2

证明:

必要性 设M为G中最大匹配，若G中存在M的可增广的交错路径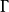，则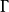在M中的边比不在M中的少1。设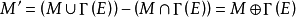(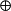为对称差运算)，则M’中边彼此不相邻且M’比M多一条边，即M’是比M多一条边的匹配，这与M是最大匹配相矛盾，所以M不含可增广的交错路径。

充分性 设M是G中不含可增广的交错路径的匹配，是G中的最大匹配，只要证明。为此，考虑和M对称差的导出子图，设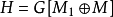。当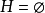(空图)时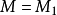，，于是M为G中最大匹配。若，由于M，都是匹配，所以H各连通分支要么是由M和中的边组成的交错圈，在交错圈上M和中的边数相等，要么为由M和中的边组成的交错路径。由已知条件可知M不含可增广的交错路径，是最大匹配，由必要性可知，中也无可增广的交错路径，于是在由M和组成的交错路径上，M和的边也相等，总之M和边的个数相同，所以M为最大匹配。2