[科普中国]-拉梅方程

简介

在数学中，拉梅函数（或椭球谐波函数）是拉梅方程（二阶常微分方程）的解。 它在论文（加布里埃尔·拉梅1837）中介绍。 拉梅方程出应用于椭圆坐标中拉普拉斯方程的变量分离方法中。在一些特殊情况下，可以用称为拉梅多项式的多项式来表示解。1

拉梅方程的公式拉梅方程的等式如下：

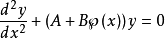
其中A和B是常数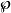，是魏尔斯特拉斯(Weierstrass)椭圆函数。 最重要的情况是当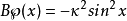和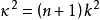对于整数n和k的椭圆模，在这种情况下，解扩展到在整个复平面上定义的拟态函数。对于B的其他值，解具有分支点。

通过用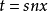将独立变量更改为t，拉梅方程也可以以代数形式重写为

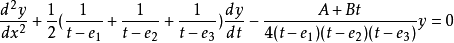
经过变化之后变成了亨恩方程的特例。

拉梅方程的更一般形式是可以写入的椭圆方程或椭圆波方程（观察我们写的是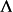，而不是上面的A）。

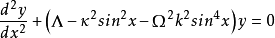
其中k是雅可比椭圆函数的椭圆模量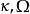，是常数。 对于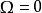，方程式成为具有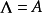的拉梅方程。对于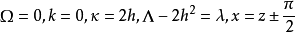方程简化为Mathieu方程

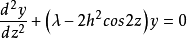
拉梅方程的威尔斯特拉斯式非常不适合于计算。方程式最合适的形式是以雅可比形式。代数和三角形的使用也很麻烦。拉梅方程出现于量子力学中，作为关于各种周期性和非调谐电位的Schrödinger方程的经典解的小波动方程。2

渐近展开Müller已经获得了对于κ的大值的周期性椭圆波函数的渐近展开，以及拉梅方程的渐近展开。他对于特征值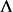获得的渐近展开是，q近似为一个奇整数（并且由边界条件更准确地确定）：

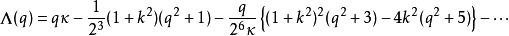
观察条件在q和k（如Mathieu函数的相应计算，扁圆球形波函数和扁圆球形波函数）中交替。具有以下边界条件（其中K（k）是由完整椭圆积分给出的四分之一周期）

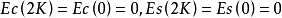
以及导数

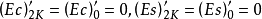
分别定义椭球波函数

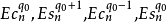
这里的上标是指Ec的解，而较低的解Es。最后在q0扩展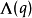，会得到：

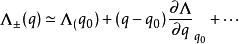
在Mathieu方程的极限中，这些表达式减少到Mathieu情况的相应表达式。3