[科普中国]-轴对称流动

流函数

我们取对称轴为柱坐标系（ ）和oz轴。则流动情况与坐标 无关，且许多情况下v=0.在轴对称流动中，不可压缩流体稳定流动的连续性方程可写成柱坐标形式得到：

或流线微分方程是：

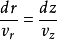
其全微分函数可写做：

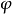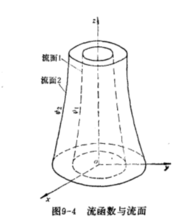
在一流线上，是常值，故称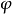为流函数。由此可以推知，在轴对称流动中，流函数在流线围绕对称轴转动所构成的曲面（即流面）上保持常数。不同的常数代表不同流线及对应的流面。2

研究情况轴对称流动最重要的情形是在直管彗中的流动，这种流动的速度剖面是抛物线型的．很早以前，Th Sexl就研究了这种流动的稳定性，他未能发现任何不稳定现象，但是他也没有能够证明对所有的Reynolds数这种流动都是稳定的．经过一段时间以后，J，Pret sch成功地证明了这种抛物线型速度剖面的稳定性可以归结为平面Couette流动(纯剪切流动)的稳定性．因为平面Couette流在所有的Reynolds数下都是稳定的，所以对圆管中速度剖面是抛物线型的流动，这个结论也是成立的。G.M.Corcoa和J.R.Sellars以及几位当前正在研究这个问题的人都得到了同样的结论，最后Th.Sexl和K.Splelberg再次证实了这个结论。由于下列两个方面的原因，这个结论是十分令人吃惊的．第一、圆管中的流动的的确确发生转动。第二，同样是抛物线型速度剖面，小扰动可以使槽中的流动变得不稳定，但是却不能使圆管中的流动失稳，这一点是很难想象的。由于这些原因，人们试图从理论和实验两方面进一步研究这个问题。3

应用实例轴对称流的一些重要的实用例子有：

1．绕超音速飞机的机身、火箭或冲压发动机的流动。

2．绕弹体的流动。

3．在圆截面管道、喷管和扩压器里的流动等。4