[科普中国]-庞加莱对偶性定理

简介

在数学中，以亨利·庞加莱（Henri Poincaré）命名的庞加莱对偶性定理是流形结构的基本结果。 它指出，如果M是一个n维定向的闭合流形（紧凑而没有边界），则M的第k个流形与M的（n-k）流形是同构的，对于所有整数k，

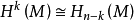
庞加莱对偶性适用于任何系数环，只要有一个取决于该系数环的方向；特别地，由于每个流形具有独特的取向模数2，所以庞加莱对偶性保持模数2而没有任何取向的假设。1

历史1893年，亨利·庞加莱首次提出了一种“庞加莱”的形式。这是说贝蒂数：闭合（即紧凑且无边界）可定向的n流形的第k和（n-k）贝蒂数相等。在那个时候，上同调的概念被澄清了大约40年。在他1895年的论文分析中，庞加莱试图用他发明的拓扑交叉理论来证明这个定理。对他的作品的批评使他意识到他的证明是有严重缺陷的。在分析情况的前两种补充中，庞加莱给出了双三角的新证明。

庞加莱对偶性在20世纪30年代出现同时性之前没有采用其现代形式。

现代表述庞加莱对偶定理的现代表述是关于流形和上同调的：如果M是闭合取向的n流形，并且k是整数，那么第k个流形就有一个规范的同构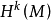 到（n-k）流形 ，在这里，同整和同调是采用整数环中的系数，但同构性适用于任何系数环。具体地说，一个将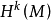 元素映射到它的卡积，它是面向M的。

对于非紧凑型的流形，必须用紧密的支持来取代上同学。

流形被定义为负的零，所以庞加莱的对偶性尤其意味着，在大于n的角度上，可定向闭合n-流形的流形和上同调群是零。

双线性配对假设M是紧密无边界和可定向的，让

表示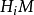 的挠子群。并且让

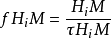
是自由部分与整数系数有关的流形。然后是双线性映射，即对偶性配对。

和

第一种形式通常称为交叉形式，第二种是扭转联接形式。 假设流形M是平滑的，则通过扰动流形类别来横向计算交叉乘积并计算它们的定向交叉数。 对于扭转链接形式，通过实现nx作为某个类z的边界来计算x和y的配对。 形式是分子的分数，z的横向交叉数与y和分母n。

配对是对偶配对的声明意味着伴随地图

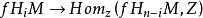
和

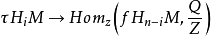
是群的同构。

这个结果是庞加莱对偶性的应用。

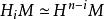
以及给出识别的通用系数定理

因此，庞加莱对偶性表示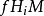和是同构的，虽然没有给出同构的自然图， 并且同样地，和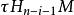也是同构的。2

概括和相关结果庞加莱对偶性定理是对边界多边形的泛化。在不定向的情况下，考虑到地方的方向，可以给出独立于定向性的声明：参见扭曲的庞加莱对偶性。

布兰奇菲尔德对偶性是庞加莱对偶性的一个版本，它提供了一个同源性的一个阿巴尔的覆盖空间的流形和相应的同态学与紧凑的支持。它用于获得关于亚历山大模块的基本结构结果，并可用于定义结点。

随着流形理论的发展，从1955年开始，包括K-理论和其他非凡的理论，一旦构建了多元化的产品，就认识到H*的流形可以被其他理论所取代。更具体地说，广义流形理论有一般的庞加莱对偶性定理，它需要一种关于流形理论的方向概念，并且是根据广义Thom同构定理来制定的。Thom同构定理在这方面可以被认为是广义流形理论的庞加莱对偶性的生发观念。

更为显着的对偶性是对（可能是单数）几何对象的适当泛化，如分析空间或方案，而交叉流形则被开发R.McPherson和M.Goresky用于分层空间，如实数或复数代数品种，庞加莱对这种分层空间的对偶性。

代数拓扑中有许多其他形式的几何对偶性，包括Lefschetz对偶性，亚历山大对偶性，Hodge对偶性和S对偶性。

更代数地，可以抽象出一个庞加莱复合体的概念，它是一个代数对象，其行为类似于一个流形的奇异链复合体，特别是在其流形上满足庞加莱对偶性，相对于基础类。庞加莱空间是一个奇异的链组合是庞加莱复合体。这些并不是所有的流形，而是它们不成为流形，可以通过阻碍理论来衡量。