概念
函数迭代法(function iteration method)亦称函数空间迭代。动态规划的求解方法之一是以段数作为参变数,先求在各个不同段数下的最优策略,然后从对应的最优解中选出最优者,从而同时确定了最优段数。
设有 个点:
个点: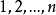 ,任意两点
,任意两点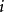 与
与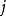 之间的距离(或行程时间,运费等)为
之间的距离(或行程时间,运费等)为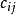 ,
,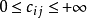 。
。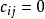 表示
表示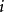 与
与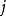 为同一点,
为同一点,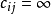 表示两点间无通路。由一点直接到另一点算作一步。要求在不限步数的条件下,找出点
表示两点间无通路。由一点直接到另一点算作一步。要求在不限步数的条件下,找出点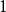 到点
到点 的最短路线。
的最短路线。
我们把类似上述不限定数的有限阶段决策问题称为阶段数不固定的有限阶段决策过程。在解此问题时可以不考虑回路,因为含有回路的路线一定不是最短路。
设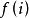 表示由点
表示由点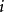 到点
到点 的最短距离,则由
的最短距离,则由 最优性原理,得:
最优性原理,得:
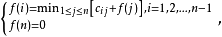 该方程是上述问题的动态规划函数的基本方程。它是关于最优值函数
该方程是上述问题的动态规划函数的基本方程。它是关于最优值函数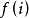 的函数方程,而不是递推关系式,这给求解带来一定的困难,下面介绍求解该方程的函数迭代法。
的函数方程,而不是递推关系式,这给求解带来一定的困难,下面介绍求解该方程的函数迭代法。
函数迭代法的基本思想是构造一个函数序列 来逼近最优值函数
来逼近最优值函数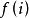 ,其算法步骤如下:
,其算法步骤如下:
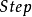
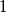 :
: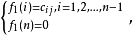 令
令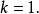
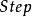
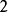 :
: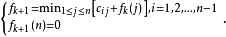
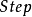
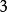 :若
:若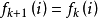 ,
,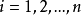 ,则令
,则令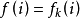 ,
,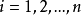 ,停;否则,令
,停;否则,令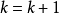 ,转
,转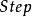
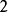 。
。
算法中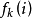 的意义十分直观,表示由
的意义十分直观,表示由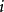 点出发,至多走
点出发,至多走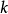 步(即经过
步(即经过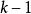 个点)到达点
个点)到达点 的最短路线的长度。因为不考虑回路,所以算法的迭代次数一定不超过
的最短路线的长度。因为不考虑回路,所以算法的迭代次数一定不超过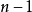 。1
。1
函数迭代法收敛性由函数迭代法的算法产生的函数序列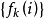 关于
关于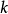 单调下降且收敛到
单调下降且收敛到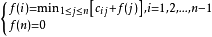 的解。
的解。
证明:任意的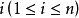 ,有
,有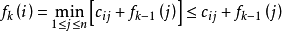 。
。
取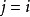 ,则
,则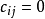 ,故
,故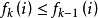 对
对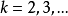 皆成立。即
皆成立。即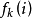 关于
关于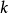 单调下降。
单调下降。
由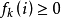 ,所以
,所以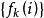 关于
关于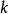 是单调有界序列,因而
是单调有界序列,因而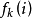 收敛,设收敛到
收敛,设收敛到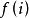 ,下面证明
,下面证明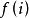 是
是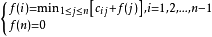 的解。
的解。
由于状态 仅取有限多个值,所以上述收敛是一致收敛。按定义,任给
仅取有限多个值,所以上述收敛是一致收敛。按定义,任给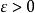 ,总存在
,总存在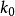 ,当
,当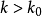 时,有
时,有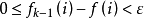 ,
,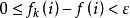 。
。
由此得:
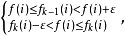 从而
从而
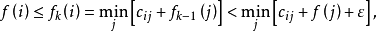
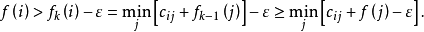 令
令 ,由上面两式有:
,由上面两式有:
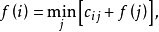 这表明
这表明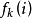 收敛到方程
收敛到方程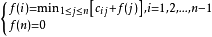 的解。1
的解。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国