[科普中国]-双曲线性映射

双曲线性映射亦称双曲线性同构，是沿一个方向扩张，沿另一个方向收缩的可逆线性映射。线性映射的双曲性经过小扰动之后不至于被破坏，这一性质在动力系统结构稳定性的研究中起着重要的作用。皮尤夫(Pugh,C.)于1969年进一步证明的结论成为哈特曼定理泛函分析方法证明的核心。

简介双曲线性映射是微分动力系统的一个有基本重要性的概念。可以说整个双曲理论从这个简单的概念开始。称有限维线性空间 E 的一个线性自同构 A 为双曲线性映射，如果 A 的所有特征值的模都不等于 1。

双曲集所谓“双曲集”的定义是，称 E 的一个线性自同构A为双曲线性映射，如果 E 分解为直和 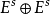，在 A 下不变，即

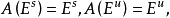
并且存在两个常数 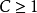和 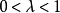使得对任意向量 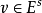以及任意非负整数 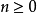都有

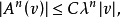同时对任意向量 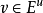以及任意非负整数 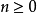都有

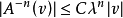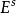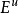粗略地说就是，E 分成两个方向 和 其中 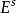的向量在A 的作用下一致指数压缩，而 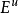的向量在A 的作用下一致指数扩张。在这个定义中，允许两种特殊情形，就是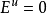或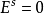的情形，也就是纯粹压缩和纯粹扩张的情形。1

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学