[科普中国]-仿射球面

仿射球面(affine hypersurface)是一个重要的超曲面，指仿射空间中仿射法线交于一点或互相平行非退化的超曲面。一个局部严格凸的仿射球称为虚的或抛物型的仿射球面，若它的仿射法线互相平行。

概念仿射球面(affine hypersurface)是一个重要的超曲面。指仿射空间中仿射法线交于一点或互相平行非退化的超曲面。一个局部严格凸的仿射球称为虚的或抛物型的仿射球面，若它的仿射法线互相平行。它称为一个真仿射球面，若它的仿射法线交于一点，称交点为它的仿射中心。真仿射球又依仿射中心位于曲面凹的一侧或凸的一侧，分别称为椭圆型的或双曲型的仿射球面。三维仿射空间A中的椭球面、双叶双曲面和椭圆抛物面分别是椭圆型、双曲型和抛物型仿射球面的例子。1

详细介绍设(x1，x2，…，xn+1)是n+1维仿射空间A中的坐标，A中的局部严格凸超曲面，局部上可表示为：xn+1=f(x1，x2，…，xn)，其中f是由定义在A中某个开集上的严格凸的可微函数。M是抛物型仿射球面的充分必要条件为f满足以下蒙日-安培方程：

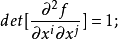M是椭圆型或双曲型仿射球面的充分必要条件为f的勒让德变换函数：

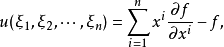
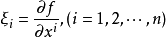
满足：

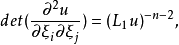其中L1为仿射平均曲率，它为常数.欧氏曲面论中法线交于一点或互相平行的曲面中有球面和平面两种，而仿射球面则广泛得多。因此，对仿射球面的分类是基本的、重要的.关于布拉施克度量完备的局部严格凸仿射球面的整体分类始于布拉施克(Blaschke，W.J.E.)，他于1923年证明：一个紧致无边的2维球面一定是椭球面.后来，戴克(Deicke，A.)于1953年把这个结果推广到了高维。因为完备的椭圆型仿射球面一定是紧致无边的，他们实际上完成了对完备椭圆型仿射球面的分类。对完备抛物型仿射球面的分类是卡拉比(Calabi，E.)完成的，他于1958年证明：一个完备的抛物型仿射球面一定是椭圆抛物面。完备的双曲型仿射球面是迷人的，它不必是二次超曲面，例如，由xx…x=1确定的超曲面，卡拉比曾构造出许多别的例子，并于1971年提出猜测：A中每个完备的双曲型仿射球面渐近于A中某个凸锥的边界；反之，任给一个负常数和A中一个非退化的凸锥，A中有惟一一个完备的双曲型仿射球面渐近于所给凸锥的边界，并以所给常数为仿射平均曲率。这个猜测，经过卡拉比、丘成桐、郑绍远、佐佐木(Sasaki，T.)等数学家的努力，直到1990年才被李安民彻底解决，从而完成了完备局部严格凸仿射球面的整体分类。关于布拉施克度量为常截面曲率的仿射球面的局部分类于1990年由弗航肯(Vrancken，L.)、李安民、西蒙(Simon，U.)完成。这类仿射球面局部地为椭球面(正截面曲率)、双曲面(负截面曲率)、椭圆抛物面和由xx…x=1定义的超曲面(零截面曲率)。对仿射球面的研究，自然地引出以下方程问题：蒙日-安培方程(*)的定义在整个A上的凸解f是二次多项式吗?或等价地，f的图是椭圆抛物面吗?答案是肯定的.n=2是约根斯(Jo¨rgens，K.)于1954年证明的；n≤5是卡拉比于1958年证明的；任意的n是波戈列洛夫(Погорелов，А.В.)于1972年证明的。2

超曲面超曲面（英语：hypersurface）是几何中超平面概念的一种推广。假设存在一个n维流形M，则M的任一(n-1)维子流形即是一个超曲面。或者可以说，超曲面的余维数为1。

在代数几何中，超曲面是指n维射影空间上的一个(n-1)维的代数集。它可由方程F=0来定义，其中F是齐次坐标下的一个齐次多项式。由于可能存在奇点，严格地说这并不是一个子流形。

在数学中，**超平面（Hyperplane）**是维欧氏空间中余维度等于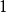的线性子空间。这是平面中的直线、空间中的平面之推广。

设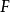为域（为初等起见，可考虑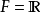）。n 维空间{\displaystyle F^{n}}中的超平面是由方程

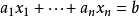定义的子集，其中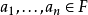是不全为零的常数。

在线性代数的脉络下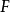，-矢量空间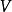中的超平面是指形如

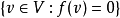的子空间，其中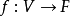是任一非零的线性映射。

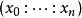
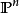在射影几何中，同样可定义射影空间中的超平面。在齐次坐标下，超平面可由以下方程定义

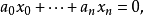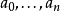其中是不全为零的常数。

射影几何在数学里，射影几何（projective geometry）研究在射影变换下不变的几何性质。与初等几何不同，射影几何有不同的设定、射影空间及一套基本几何概念。直觉上，在一特定维度上，射影空间比欧氏空间拥有“更多”的点，且允许透过几何变换将这些额外的点（称之为无穷远点）转换成传统的点，反之亦然。

射影几何中有意义的性质均与新的变换概念有关，此一变换比透过变换矩阵或平移（仿射变换）表示的变换更为基础。对几何学家来说，第一个问题是要找到一个足以描述这个新的想法的几何语言。不可能在射影几何内谈论角，如同在欧氏几何内谈论一般，因为角并不是个在射影变换下不变的概念，如在透视图中所清楚看到的一般。射影几何的许多想法来源来自于对透视图的理论研究。另一个与初等几何不同之处在于，平行线可被认为会在无穷远点上交会，一旦此一概念被转换成射影几何的词汇之后。这个概念在直观上，正如同在透视图上会看到铁轨在水平线上交会一般。

虽然这些想法很早以前便已存在，但射影几何的发展主要还是到19世纪才开始。大量的研究使得射影几何变成那时几何的代表学科。当使用复数的坐标（齐次坐标）时，即为研究复射影空间之理论。一些更抽象的数学（包括不变量理论、代数几何意大利学派，以及菲利克斯·克莱因那导致古典群诞生的爱尔兰根纲领）都建立在射影几何之上。此一学科亦吸引了许多学者，在综合几何的旗帜之下。另一个从射影几何之公理化研究诞生的领域为有限几何。

射影几何的领域又可细分成许多的研究领域，其中的两个例子为射影代数几何（研究射影簇）及射影微分几何（研究射影变换的微分不变量）。3

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学