[科普中国]-非线性薛定谔方程

简介

当势场依赖于波函数时，就导出了非线性薛定谔方程，其一般形式为

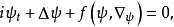
其中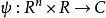，是复值函数。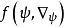为是非线性作用项，典型的情形为：

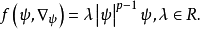
当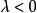时称为聚焦型（focusing）；

当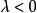时称为非聚焦型（defocusing ）。

除了量子力学之外，非线性薛定谔方程还可以用来描述物理中的各种非线性波，如激光束在折射率与波幅有关的介质中的传播、理想流体在自由上的水波、等离子波等。

薛定谔方程[Schrodinger equation]

薛定谔方程是量子力学中的基本方程，它与相应的附加条件一起，决定表征量子系统状态的波函数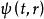。对于非相对论性且无自旋粒子的系统，首先由薛定谔在1926年导出，其形式为

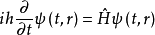其中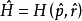，是哈密顿算子。算子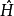按以下通则构造：在经典哈密顿函数H(p，r)中将粒子动量 p 及其坐标 r 用相应算子代替，在坐标表象和动量表象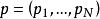中，它们分别具有如下形式：

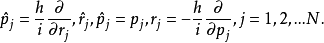
对于由矢势A（t，r）表征的电磁场中（电量为 e ）的带电粒子，动量 p 要有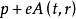代替（国际单位制）。在这些表象中，薛定谔方程是一个偏微分方程，如对势场U(r)中的粒子，相应的波函数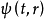满足

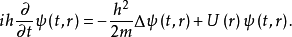
将薛定谔方程推广到具有自旋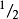的非相对论粒子的情况（二分量函数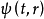）称为泡利方程（Pauli equation）；推广到具有自旋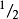的相对论粒子的情况（四分量函数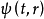）称为狄拉克方程（Dirac equation）；推广到无自旋的相对论粒子的情况称为克莱因方程（Klein-Gordon equation）；推广到自旋为 1 的相对论粒子的情况（函数是一向量）称为普罗卡方程（Proca equation）。1