[科普中国]-欧拉类

欧拉类(Euler class)是实向量丛底空间的一个上同调类。定向实n维向量丛ξ的欧拉类是上同调类e(ξ)∈Hn(B;Z)，在标准同构 π*:Hn(B;Z)→Hn(E;Z)下，它对应于u|E，其中u是Hn(E1E0)中惟一的上同调类，限制在Hn(F1F0)中是标准的定向类。这里的E为全空间，B为底空间。

基本介绍欧拉类是实向量丛底空间的一个上同调类，定向实n维向量丛的欧拉类是上同调类，在标准同构

下，它对应于，其中u是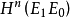中惟一的上同调类，限制在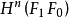中是标准的定向类。这里的为全空间，为底空间。

欧拉类的性质欧拉类的性质：

1．自然性。若被一个保定向的丛映射覆盖，则。

2．若把的定向反向，则欧拉类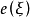变号。

3．若纤维维数n是奇数，则

4．自然同态把欧拉类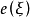变为施蒂费尔一惠特尼类。

5．惠特尼和的欧拉类满足。类似地，笛卡儿积的欧拉类满足

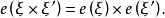
6．若定向向量丛具有一个处处为零的截面，则其欧拉类必为零。

相关概念示性类纤维丛通常用一些拓扑不变的整数(称为示性数)来标志其和平庸丛的偏离，当我们引人联络以后，这些示性数可以用由联络表示的示性类在整个底流形上的积分表示出来。但积分的结果(示性数)与联络的选择无关，是拓扑不变量。在纤维丛上可以定义很多不同的示性类，如斯蒂弗尔-惠特尼类、庞特里亚金(Pontrjagin)类、陈(陈省身)类和欧拉类等。对于2n维黎曼流形，欧拉类定义为

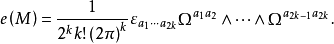欧拉类对底流形积分即得欧拉数

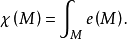此即高斯-博内(Gauss-Bonnet)定理，是更一般的阿蒂亚-辛格(Atiyah-Singer)指标定理的特例1。

陈(省身)类陈(省身)类(Chern class)是复向量丛的一种上同调类。设ω为复n维向量丛，为其基本实向量丛，表中所有非零向量所成子空间，中任意点位于ω的一个确定的纤维中。设ω上给定埃尔米特度量，取在中的正交补作为点上的纤维，得以为底空间的复n-1维向量丛，则陈类按ω的复维数递推地定义为：顶陈类(即最高维陈类)等于欧拉类；对in，类。

这种定义是有意义的，因为在古津序列中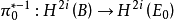，对于i