斯廷罗德运算(Steenrod operation)上同调群中一种特定的加法同态。斯廷罗德运算由四个基本性质定义。
简介概述斯廷罗德运算是上同调群中一种特定的加法同态。
具体内容斯廷罗德运算由下述四个基本性质定义,这里系数群理解为Z/2。
1、对于每一对空间X⊃Y,和每一对非负整数n,i,定义一个加法同态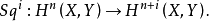
2、自然性。若f:(X,Y)→(X',Y'),则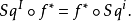
3、若a∈Hn(X,Y),则sq0(a)=a,Sqn(a)=a∪a,而sqi(a)=0(i>n)。因此,最有意义的运算是0
斯廷罗德运算(Steenrod operation)上同调群中一种特定的加法同态。斯廷罗德运算由四个基本性质定义。
简介概述斯廷罗德运算是上同调群中一种特定的加法同态。
具体内容斯廷罗德运算由下述四个基本性质定义,这里系数群理解为Z/2。
1、对于每一对空间X⊃Y,和每一对非负整数n,i,定义一个加法同态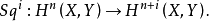
2、自然性。若f:(X,Y)→(X',Y'),则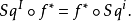
3、若a∈Hn(X,Y),则sq0(a)=a,Sqn(a)=a∪a,而sqi(a)=0(i>n)。因此,最有意义的运算是0
 扫码下载APP
扫码下载APP

