对于多目标规划问题
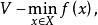 引进它的由较多序定义的两个解,并且讨论这些解的有关基本性质,(VMP)的可达目标集
引进它的由较多序定义的两个解,并且讨论这些解的有关基本性质,(VMP)的可达目标集
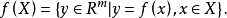
定义1 设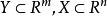 和XcR“是非空集合,
和XcR“是非空集合,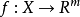 。
。
(1) 若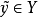 ,并且不存在
,并且不存在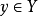 使得
使得
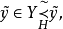 则称
则称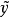 是集合
是集合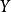 的较多有效点。Y的所有较多有效点组成的集合记作
的较多有效点。Y的所有较多有效点组成的集合记作 ,若
,若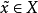 并且
并且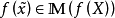 ,则称
,则称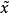 是多目标规划问题(VMP)的较多有效解。(VMP)的所有较多有效解组成的集合记作
是多目标规划问题(VMP)的较多有效解。(VMP)的所有较多有效解组成的集合记作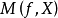 。
。
(2) 若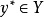 ,并且
,并且
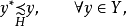 则称
则称 是集合
是集合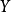 的较多最优点,
的较多最优点,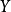 的所有较多最优点组成的集合记作
的所有较多最优点组成的集合记作 。若
。若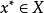 并且
并且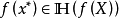 ,则称
,则称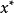 是多目标规划问题(VMP)的较多最优解。(VMP)的所有较多最优解组成的集合记作
是多目标规划问题(VMP)的较多最优解。(VMP)的所有较多最优解组成的集合记作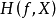 。
。
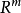 中集合的较多有效点是在较多序意义下该集合中不存在比它更好点的点,从而(VMP)的较多有效解即是在较多序意义下它的约束集中不存在比它更好解的解。(VMP)的较多有效解就是对于它的向量目标中的较多个目标而言是非劣的解。
中集合的较多有效点是在较多序意义下该集合中不存在比它更好点的点,从而(VMP)的较多有效解即是在较多序意义下它的约束集中不存在比它更好解的解。(VMP)的较多有效解就是对于它的向量目标中的较多个目标而言是非劣的解。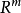 中集合的较多最优点是在较多序意义下该集合中的最好点,(VMP)的较多最优解即在较多序意义下它的约束集中的最好解。(VMP)的较多最优解也即对其向量目标中较多个目标而言是最优的解。
中集合的较多最优点是在较多序意义下该集合中的最好点,(VMP)的较多最优解即在较多序意义下它的约束集中的最好解。(VMP)的较多最优解也即对其向量目标中较多个目标而言是最优的解。
定理1 设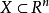 是非空集合,
是非空集合,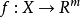 。
。
(1)若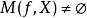 ,则
,则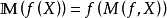 。
。
(2)若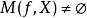 ,则
,则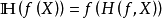 。
。
定理2 设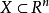 是非空集合,
是非空集合,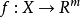 ,记
,记
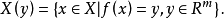
(1) 若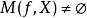 ,则
,则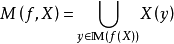 。
。
(2) 若 ,则
,则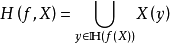 。
。
下面给出较多有效点(解)和较多最优点(解)的一个充要条件。
定理3设 和
和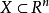 是非空集合,
是非空集合,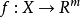 。
。
(1) 当且仅当
当且仅当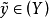 并且
并且
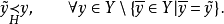
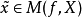 当且仅当
当且仅当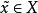 并且
并且
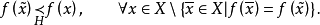
(2)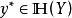 当且仅当
当且仅当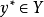 并且不存在
并且不存在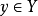 使得
使得
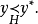
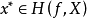 当且仅当
当且仅当 并且不存在
并且不存在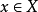 使得
使得
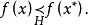
从此定理可以知道,多目标规划问题(VMP) 的较多有效解和较多最优解也即在严格偏爱“ ”意义下的最优解和非劣解。因此,它们也可分别叫做问题(VMP)的强较多最优解和弱较多有效解。
”意义下的最优解和非劣解。因此,它们也可分别叫做问题(VMP)的强较多最优解和弱较多有效解。
定理4 任一较多有效点(解)必是较多最优点(解),并且它们都是Pareto有效点(解)。
定理5设 和
和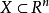 是非空集合,
是非空集合,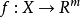 ,
,
(1) 若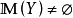 ,则
,则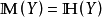 。
。
(2) 若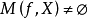 ,则
,则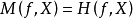 。
。
定理6设 和
和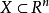 是非空集合,
是非空集合,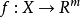 ,
,
(1) 若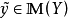 ,则
,则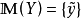 。
。
(2) 若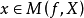 ,则
,则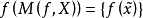 。
。
定理7设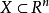 是非空凸集,
是非空凸集,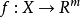 是严格凸向量函数,若
是严格凸向量函数,若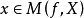 ,则
,则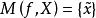 。
。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国