[科普中国]-可行下降方向

研究问题

对约束优化问题（非线性规划问题NLP）

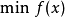
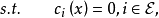(1)

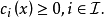记可行集

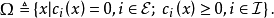
对约束优化问题的最优值点，一个显然的结论是该点在可行域内部不能含有下降方向。

可行下降方向的定义定义一若可行方向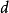满足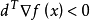，则称d为约束优化问题(1)在x点的可行下降方向。

定义二设X是非线性规划问题(NLP)的一个可行点，非零矢量d即是点X处的可行方向，又是f(X)在点X处的一个下降方向，则称d为f(X)在点X处的一个可行下降****方向。1

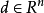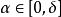可行方向定义称为约束优化问题(1)在x点的可行方向，若存在，对任意，有。

可行方向的基本性质若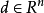为约束优化问题(1)在x点的可行方向，则2

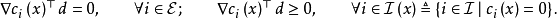证明: 由于一个等式约束可以等价地表示成两个不等式约束，为此，我们只考虑含有不等式约束的情形，若结论不成立，则存在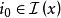，使得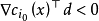，从而对充分小的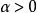有

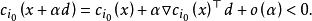这与d为约束优化问题(1)在x点的可行方向矛盾。 证毕。

对约束为线性的情况，上述结论的逆命题也成立，借助可行方向，容易建立约束优化问题的下述性质。

相关定理定理1设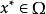是约束优化问题(1)的局部最优解，则点的任一可行方向d满足。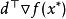

该结论是说，在约束优化问题的最优值点不存在可行下降方向。

利用定理1，并结合稳定点的定义，我们可以得到下面的结论：

定理2若约束优化问题(1)的可行域为闭凸集，则其任一局部最优解为其稳定点。

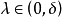下降方向定义设x是(NLP)的一个可行点(可行域中的点)，若存在非零矢量d满足：存在，当时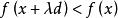，则称d为f(x)在点x处的一个下降方向。 1