整体介绍
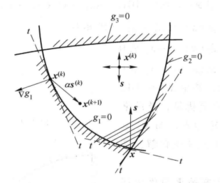
一个设计点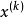 在可行域内是一个自由点,即在各个方向上都可以作出移动得到新点,如图1所示,但一旦当设计点
在可行域内是一个自由点,即在各个方向上都可以作出移动得到新点,如图1所示,但一旦当设计点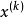 处于一个起作用约束上时,它的移动就会受到可行性的限制。此时
处于一个起作用约束上时,它的移动就会受到可行性的限制。此时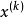 点的可行方向s必满足2
点的可行方向s必满足2
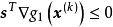 条件,因为要使新点
条件,因为要使新点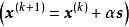 在
在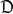 内,必满足
内,必满足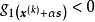 ,由于
,由于
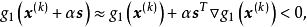 其中
其中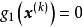 ,且对于充分小的常数
,且对于充分小的常数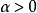 ,故式
,故式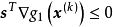 必定成立。此时,可行方向s与约束梯度向量
必定成立。此时,可行方向s与约束梯度向量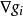 的夹角大于90°,如图1所示。2
的夹角大于90°,如图1所示。2
式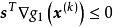 的极限情况是取等号,这时有
的极限情况是取等号,这时有
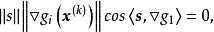 即可行方向s与该点的约束梯度向量
即可行方向s与该点的约束梯度向量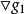 垂直,也就是说,该点的可行方向就是该点约束面的切线方向t—t。
垂直,也就是说,该点的可行方向就是该点约束面的切线方向t—t。
当某个设计点同时有几个约束起作用时,如图1中的x点是约束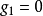 和约束
和约束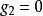 约束面的交点,其可行方向集合
约束面的交点,其可行方向集合
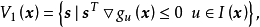 即图中的阴影线内的任一方向都是可行方向。同理,当既有不等约束的起作用约束集合又有等式约束集合时,其x点的可行方向集合为:2
即图中的阴影线内的任一方向都是可行方向。同理,当既有不等约束的起作用约束集合又有等式约束集合时,其x点的可行方向集合为:2
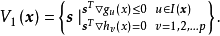
产生可行方向的条件可行方向是指沿该方向作微小移动后,所得到的新点是可行点,且目标函数值有所下降。显然,可行方向应满足可行和下降两个条件。
可行条件方向的可行条件是指沿该方向作微小移动后,所得到的新点为可行点。若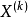 点在一个约束面上,对
点在一个约束面上,对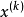 点作约束面
点作约束面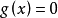 的切线
的切线 ,显然满足可行条件的方向
,显然满足可行条件的方向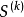 应与起作用的约束函数在
应与起作用的约束函数在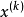 点的梯度
点的梯度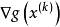 的夹角大于或等于90°。
的夹角大于或等于90°。
下降条件方向的下降条件是指沿该方向作微小移动后,所得新点的目标函数值是下降的,满足下降条件的方向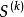 应和目标函数在
应和目标函数在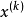 点的梯度
点的梯度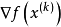 的夹角大于90°。3
的夹角大于90°。3
可行方向的产生方法满足可行和下降条件的方向在可行下降方向区内,则在该区内寻找一个最有利的方向作为本次迭代的搜索方向,关于这个方向的产生方法主要有随机产生法、线性规划法和梯度投影法几种,具体方法及过程可参考后文相关参考书籍。3
随机产生法这种方法从原理上讲与随机方向搜索法产生的方法基本相同。先在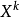 点产生N个随机单位方向向量
点产生N个随机单位方向向量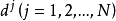 ,然后将产生的N个方向逐个进行可行性和下降条件的检验,用这种方法产生适用可行方向的优点是比较简单,容易实现程序化。
,然后将产生的N个方向逐个进行可行性和下降条件的检验,用这种方法产生适用可行方向的优点是比较简单,容易实现程序化。
线性规划法这种方法对线性和非线性的不等式约束优化问题均适应,但不能容纳等式约束,是可行方向法中选择适用可行方向的主要方法之一。这种方法的要点是:在可行下降扇形区内选择一方向d进行搜索,可得到一个目标函数值下降的可行点。3
梯度投影法梯度投影法有时也称为大步梯度法,主要用于求解线性约束优化问题。当沿约束面进行寻优搜索时,需要确定一个沿约束面运动的适用可行方向。3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国