基本介绍
约束最优化问题(constrained optimization problem)是指具有约束条件的非线性规划问题。极小化问题的一般形式为
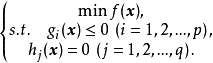 仅有等式约束条件的约束最优化问题,可采用消元法、拉格朗日乘子法或罚函数法,将其化为无约束最优化问题求解;对于含有等式约束和不等式约束条件的最优化问题,可采用以下方法:将不等式约束化为等式约束;将约束问题化为无约束问题;将非线性规划问题用线性逼近的方法来近似求解;在可行域中沿某方向作一维搜索,寻求最优解1。
仅有等式约束条件的约束最优化问题,可采用消元法、拉格朗日乘子法或罚函数法,将其化为无约束最优化问题求解;对于含有等式约束和不等式约束条件的最优化问题,可采用以下方法:将不等式约束化为等式约束;将约束问题化为无约束问题;将非线性规划问题用线性逼近的方法来近似求解;在可行域中沿某方向作一维搜索,寻求最优解1。
约束最优化问题的解法约束最优化问题就是求目标函数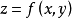 满足约束条件
满足约束条件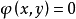 的极值问题。因此,约束最优化,也称条件极值2。
的极值问题。因此,约束最优化,也称条件极值2。
约束最优化问题的解法有两种:
化约束最优化问题为无约束最优化问题例1 最大面积 设长方形的长、宽之和等于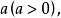 问长方形的长、宽如何设计,才能使面积最大?
问长方形的长、宽如何设计,才能使面积最大?
解: 这就是一个约束最优化问题:设长方形的长为x,宽为y,求目标函数A=xy在条件x+y=a之下的最大值。
由于从约束条件x+y=a中容易解出y=a-x,代入目标函数
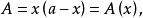 问题归结为求一元函数A(x)的极值。
问题归结为求一元函数A(x)的极值。
由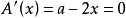 ,得驻点
,得驻点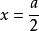 。这是实际问题,最值一定存在,则
。这是实际问题,最值一定存在,则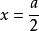 就是最大值点。因此,当
就是最大值点。因此,当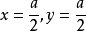 时,长方形面积最大,其最大值为
时,长方形面积最大,其最大值为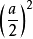 。
。
从上述例子可以看出化约束最优化问题为无约束最优化问题的思路:从约束条件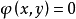 中解出
中解出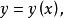 并将它代人目标函数
并将它代人目标函数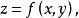 于是,问题就转化为求一元函数
于是,问题就转化为求一元函数
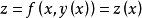 的无约束最优化问题。
的无约束最优化问题。
但是,这种方法有局限性,因为有时从约束条件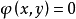 中解出y或x并非易事。因此,下面介绍另一种方法2。
中解出y或x并非易事。因此,下面介绍另一种方法2。
拉格朗日乘数法这一方法的思路是:把求约束最优化问题转化为求无约束最优化问题,看它应该满足什么样的条件?
设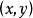 是函数
是函数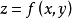 在约束条件
在约束条件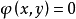 下的约束最优化问题的极值点。如果函数
下的约束最优化问题的极值点。如果函数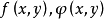 在点(x,y)的邻域内有连续偏微商,且
在点(x,y)的邻域内有连续偏微商,且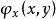 、
、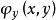 不全为0(不妨设
不全为0(不妨设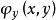 ≠0),则根据费马引理,一元函数
≠0),则根据费马引理,一元函数 在点x的微商
在点x的微商
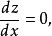 由隐微分法,有
由隐微分法,有
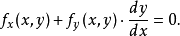 而
而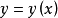 是由
是由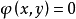 所确定,所以
所确定,所以
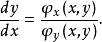 代入上式,消去
代入上式,消去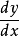 ,得
,得
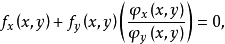 即
即
 令
令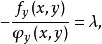 则有
则有
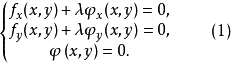 称满足此方程组(1)的点(x,y)为可能极值点。
称满足此方程组(1)的点(x,y)为可能极值点。
为了便于记忆,并能容易地写出方程组(1),我们构造一个函数
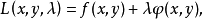 称
称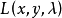 为拉格朗日函数。则方程组(1)可以记为
为拉格朗日函数。则方程组(1)可以记为
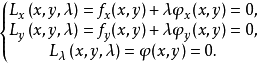
于是,我们把用拉格朗日乘数法求解约束最优化问题的步骤归纳如下:
①构造拉格朗日函数
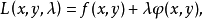
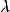 称为拉格朗日乘数;
称为拉格朗日乘数;
②解方程组
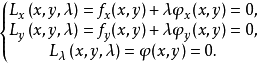 得点(x,y)为可能极值点;
得点(x,y)为可能极值点;
③根据实际问题的性质,在可能极值点处求极值2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国