[科普中国]-多项式插值法

定义

在数值分析中，多项式插值法是通过多项式对给定数据集的插值：给定一些点，找到一个正好穿过这些点的多项式。

给定一组n+1个数据点(xi,yi)，其中没有任何2个xi是相同的，是在大多数n中寻找一个多项式p，

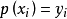， i=0,...,n。

唯一可解性定理表明这样的多项式p存在且是唯一的，并且可以通过范德蒙矩阵来证明，如下所述。

定理指出，对于n + 1插值节点(xi)，多项式插值定义了线性双射。

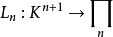
Πn是多项式的向量空间(在任何时间间隔定义包含节点)，其最多为n。

构造插值多项式假设插值多项式方程如下图形式，

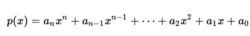
p插值点意味着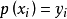，所有i∈{0,1,..,n}。

如果我们把插值多项式方程代入，我们得到一个线性方程的系数ak。得到矩阵-向量形式为

我们要用这个方程组来构造插值p(x)左边的矩阵通常被称为范德蒙矩阵。

范德蒙矩阵的条件数可能很大2，当计算系数ai时，如果使用高斯消除来求解方程组，则会导致较大的误差。

因此，一些作者提出了利用范德蒙德矩阵的结构来计算O(n2)运算中的数字稳定解的算法，而不是高斯消去法所要求的O(n3)3。这些方法依赖于首先构造一个多项式的牛顿插值，然后将其转换成上面的单项。

或者，我们可以立即用拉格朗日多项式来写多项式:

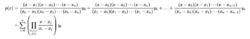
对于矩阵参数，这个公式叫做Sylvester公式，矩阵的拉格朗日多项式是弗罗贝尼乌斯协变。

多项式插值法分类为了在n阶多项式的向量空间Πn中构造唯一插值多项式。当使用Πn的单项式时，必须求解范德蒙德矩阵来构造插值多项式的系数ak。这可能是一个非常复杂的操作（按照计算机尝试做这个工作的时钟周期计算）。通过选择Πn，可以简化系数的计算，但是当用单项式表示内插多项式时，必须进行额外的计算。

1、一种方法是以牛顿形式的多项式插值法，并使用分差法来构建系数，例如，内维尔的算法。则将大量花费在O(n2)运算，而高斯消除则花费在O(n3)运算。此外，如果在数据集中添加额外的点，则只需要执行O(n)个额外的计算，而对于其他方法，则必须重做整个计算。

2、另一种是使用拉格朗日形式的多项式插值法。 所得公式立即显示插值多项式存在于上述定理中所述的条件下。 当对计算多项式的系数不感兴趣时，在计算p（x）的值（给定的x不在原始数据集中）时，拉格朗日公式将优于范德蒙德公式。 在这种情况下，我们可以将复杂度降低到O(n2)4。

应用1、其中多项式可用于近似复杂的曲线，例如排版中的字母形状（需要提供几点）。

2、自然对数和三角函数的评估：选择一些已知的数据点，创建一个查找表，并在这些数据点之间插值。多项式插值也成为数字正交和数值常微分方程中的算法和安全多方计算秘密共享方案的基础。

3、多项式插值是执行次二次乘法和平方的必要条件（例如Karatsuba乘法和Toom-Cook乘法），其中一个多项式的插值，它定义了乘积本身的乘积。例如，给定a = f（x）= a0x0 + a1x1 + ...和b = g（x）= b0x0 + b1x1 + ...，乘积ab等价于W(x)= f(x)g(x)。通过将x代入f(x)和g(x)中，沿W（x）找到点，并在曲线上得到这些点。基于这些点的插值，将产生W（x）的项和随后的乘积ab。在Karatsuba乘法的基础上，即使对于中等规模的输入，该技术也比二次乘法更快。在并行硬件实现时尤其如此。

工程技术中的应用在工程技术中，经常会遇到插值之类的计算问题，例如在半导体技术中，设计晶体管和分析其性能时，常常涉及到与半导体的杂质浓度有关的参量；在温度自动控制系统中的热电偶和温度的对应关系，当采用计算机辅助分析和控制时，必须将这些关系曲线离散化，由于这些曲线很多都是通过经验获得的，无法用函数解析表示，如单晶硅电阻率与掺杂浓度换算表，热电偶与温度的分度表。一般来讲，不是将所有数据都存人计算机，而是取一系列数值利用通常的牛顿插值法、拉格朗日插值法等，求得对应于x的y值，这些插值法都构造一个多项式，用其近似已知的或未知的函数关系的解析表达式。

在计算过程中，如果插值的数据很多，则需要大量的计算时间，这对于大型项目或实时性计算，显得很不利。查表方法可以提高运算速度，但需要较多的内存存放数据，而且无法得到任意值。

在半导体技术中，硅单晶珍杂浓度与电阻率关系，变化范围达到几个数量级，直接使用上述播值法不可能得到满意的结果。

另一个问题，如果知道y值，欲求x值。使用一组数据是做不到的，这样又会加重系统的负担。

解决上述问题的基本思想是直接用一个多项式函数近似表示未知的函数关系，这样就可以求得该函数定义域内的任意值。为了与上述插值方法以示区别，故称为“多项式插值法”。

插值多项式是广为人知的，无论何种插值方法实质上都是构造一个n阶多项式。当然，多项式的形式和构造方法可以是多种多样的。5