[科普中国]-阿贝尔函数方程

人物简介

阿贝尔是挪威数学家。生于挪威西南海岸斯塔万格附近的小岛芬岛(Finno¨y)，卒于阿伦达尔(Arendal)附近的弗鲁兰(Froland)。父亲是一个基督教牧师。阿贝尔幼年丧父，家境贫困，但他从小酷爱数学。16岁起自学当时的数学名著，中学时被誉为“数学迷”，得到教师霍尔姆博(Holmboe，B.M.)的赏识和资助。1821年以公费考入克里斯蒂安尼亚(Christiania)大学，1825年大学毕业后，获得奖学金前往柏林和巴黎留学并谋职。在德国期间，他结识了克雷尔(Crelle，A.L.)，他们共同创办了《克雷尔数学杂志》，并在前三卷上发表了22篇有关方程论、椭圆函数论和幂级数方面的著名论文，使《克雷尔数学杂志》获得很高的声誉.在巴黎他又写出一批重要论文。1827年回国，在克里斯蒂安尼亚大学任教，不久患肺结核，1829年被聘为柏林大学教授，但未到任即病逝，年仅27岁。

阿贝尔一生虽然短暂，却在数学史上留下了光辉的一页。自从16世纪三、四次方程得到解决之后，五次以上方程的根式求解问题吸引着众多的科学家。200多年未能成功，这使人们悟到了它的不可能性，在拉格朗日(Lagrange，J.-L.)和鲁菲尼(Ruffini，P.)之后，阿贝尔进一步严格地证明了一般五次方程不可能用根式求解，开辟了近世代数方程论的道路，采用了包括群论和方程的超越函数解法.1826年，他在《克雷尔数学杂志》创刊号上发表了震动数学界的论文《论代数方程，证明一般五次方程的不可解性》。他还同德国数学家雅可比(Jacobi，C.G.J.)共同奠定了椭圆函数论的基础，创立了数学的一个新分支。阿贝尔发现了椭圆函数的加法定理、双周期性，引进了阿贝尔积分。此外，在交换群、二项级数的严格理论、级数求和等方面都有突破性贡献，但可惜他的论文的价值没有及时被学术界所认识。2

施罗德函数方程施罗德函数方程是一类函数方程。函数方程：3

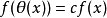称为施罗德函数方程，其中θ(x)是已知函数，c是常数。如果f1(x)是一特解(f1≠0)，则其通解为f(x)=f1(x)φ(x)，其中φ(x)是φ(θ(x))=φ(x)的通解。假设存在点a使得θ(a)=a， 并且θ(x)和f(x)在点a的邻域内可微，于是有f′(a)=0或θ′(a)=c。考查θ′(a)=c的情形，若θ(x)在x=a处二次可微，且|c|1，则令θ(x)=u， 那么在u=a的邻域f(θ(u))=cf(u)，这就化为|c|