加性函数方程(additive functional equation)是一类最简单的函数方程,所谓加性函数方程,是指形如f(x+y)=f(x)+f(y)的方程。
基本介绍形如
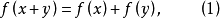 的加性函数方程,柯西(A.-L.Cauchy)证明了方程(1)的连续解只有
的加性函数方程,柯西(A.-L.Cauchy)证明了方程(1)的连续解只有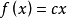 (
( 是常数),即使只要求
是常数),即使只要求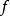 在某点连续,在该点邻域有界或可测,也只有解
在某点连续,在该点邻域有界或可测,也只有解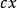 。但在非可测函数类中,哈默尔(G.K.W.Hamel)和勒贝格(H.L.Lebesgue)证明了除
。但在非可测函数类中,哈默尔(G.K.W.Hamel)和勒贝格(H.L.Lebesgue)证明了除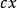 外还有无穷多个解。另一方面,奥斯特罗格拉茨基(М.В.Остроградский)证明了,如果方程(1)的解
外还有无穷多个解。另一方面,奥斯特罗格拉茨基(М.В.Остроградский)证明了,如果方程(1)的解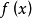 在一个正测度集合上不取两个相异值之间的值,则
在一个正测度集合上不取两个相异值之间的值,则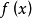 必是连续的。以上结论可以推广到n个变量的情形。方程(1)的变形方程是
必是连续的。以上结论可以推广到n个变量的情形。方程(1)的变形方程是
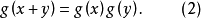 如果存在
如果存在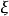 使得
使得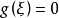 ,则
,则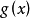 恒为零。因此假定
恒为零。因此假定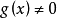 ,取
,取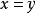 即可看出
即可看出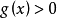 ,令
,令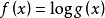 ,则方程(2)可化为方程(1)。因此,方程(2)的连续解只有
,则方程(2)可化为方程(1)。因此,方程(2)的连续解只有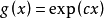 。再考虑方程
。再考虑方程
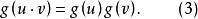 如果存在
如果存在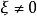 使得
使得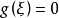 ,则
,则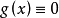 ,因此,假定
,因此,假定 时
时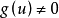 。对于
。对于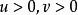 ,令
,令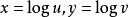 ,于是方程(3)就化为方程(2),又在方程(3)中取
,于是方程(3)就化为方程(2),又在方程(3)中取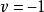 得到
得到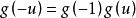 ,所以
,所以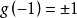 ,于是方程(3)的连续解是
,于是方程(3)的连续解是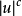 或
或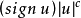 。
。
一般加法定理一般加法定理(general addition theorem)是刻画一种特殊方程存在连续的非零解特征的一个定理,一般加法定理如下:如果方程
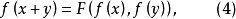 在
在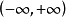 中存在连续的非常数解
中存在连续的非常数解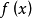 ,那么
,那么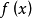 必是严格单调函数,而
必是严格单调函数,而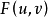 是关于
是关于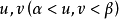 的严格单调递增连续函数,且
的严格单调递增连续函数,且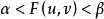 ,还存在一个
,还存在一个 ,使得
,使得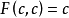 ,而且关于
,而且关于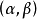 中的任意的
中的任意的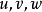 ,成立恒等式
,成立恒等式
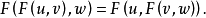 反之,如果
反之,如果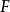 是具有这些性质的函数,则(4)式存在在
是具有这些性质的函数,则(4)式存在在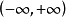 上连续的非常数解,而且若
上连续的非常数解,而且若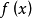 是这样的一个解,则
是这样的一个解,则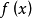 就给出了其他的解,如果
就给出了其他的解,如果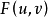 还是连续可微的,则
还是连续可微的,则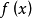 就是微分方程
就是微分方程
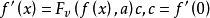 在初始条件f(0)=a下所得到的解1。
在初始条件f(0)=a下所得到的解1。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国