[科普中国]-代数算子方程

代数算子方程指算子满足一定代数关系式的算子方程。奇异积分方程的理论也可以抽象为代数算子方程去研究。

简介代数算子方程指算子满足一定代数关系式的算子方程。奇异积分方程的理论也可以抽象为代数算子方程去研究。

代数算子代数算子 S 是指巴拿赫空间 X 到巴拿赫空间 Y 的、满足一定代数关系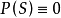的算子。P通常是多项式

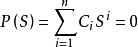但不满足低于 n 次的多项式，则称 S 为 n 次代数算子，例如

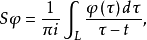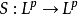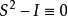L 是闭围线，则 满足方程，但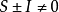，故柯西奇异积分算子是二次代数算子，又如，希尔伯特空间的投影算子 P，满足方程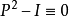，但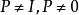，故它是二次代数算子。

再如，傅里叶积分算子

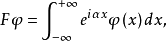
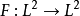满足方程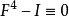，但不满足低于四次的方程，它是四次代数算子。

定义利用拉格朗日插值多项式可由 n 次代数算子 S 构造出投影算子：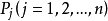

其中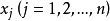 表示 P(x)=0 的 n 个单根，“∧“号表示缺少该项，则 Pj 满足：

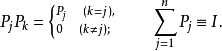由代数算子组成的下面方程

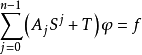称为代数算子方程，其中 S 是 n 次代数算子，Aj 是满足一定条件的系数算子，T 是紧算子，f 是已知函数。奇异积分方程可看做代数算子方程。

例如，柯西奇异积分方程是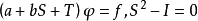，它是二次代数算子方程。在满足一定条件下，代数算子叶是诺提算子。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学