[科普中国]-卷积方程

卷积

在泛函分析中，卷积、旋积或摺积(英语：Convolution)是通过两个函数f 和g 生成第三个函数的一种数学算子，表征函数f 与g经过翻转和平移的重叠部分的面积。

如果将参加卷积的一个函数看作区间的指示函数，卷积还可以被看作是“滑动平均”的推广。

褶积(又名卷积)和反褶积(又名去卷积)是一种积分变换的数学方法,在许多方面得到了广泛应用。用褶积解决试井解释中的问题，早就取得了很好成果；而反褶积，直到最近，Schroeter、Hollaender和Gringarten等人解决了其计算方法上的稳定性问题，使反褶积方法很快引起了试井界的广泛注意。有专家认为，反褶积的应用是试井解释方法发展史上的又一次重大飞跃。他们预言，随着测试新工具和新技术的增加和应用，以及与其它专业研究成果的更紧密结合，试井在油气藏描述中的作用和重要性必将不断增大。2

卷积方程卷积方程(convolution equation)一种最常见的奇异积分方程。第二类卷积方程是指方程：

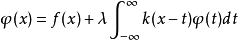
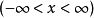
其中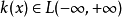：，当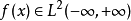，并满足条件：

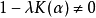其中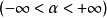：时，卷积方程可以直接利用傅里叶变换得到它在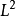中的解：

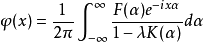
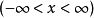
其中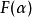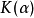，分别是f(x)和k(x)的傅里叶变换，这个解也可以写成预解核的形式：

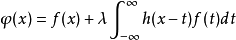其中h(x)是的傅里叶逆变换。第二类卷积方程的齐次方程可能有非零解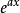，只要a满足：

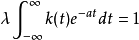因而对某些核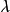，会产生连续谱，所以卷积方程不是弗雷德霍姆积分方程，第一类卷积方程是指方程3

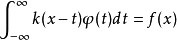
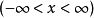
它与第二类卷积方程无本质区别，当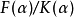属于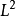时，它的解是：

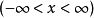
卷积方程中的积分算子：

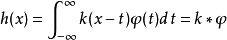称为卷积算子。当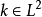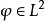，时，卷积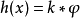总是连续函数。当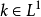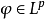，时，恒有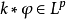，并且有豪斯多夫杨不等式：

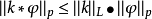在卷积方程中，作为特例，设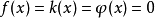，当x