[科普中国]-斐波那契搜索

引言

在介绍斐波那契查找算法之前，先介绍一下很它紧密相连的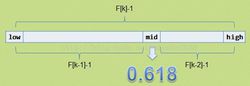一个概念——黄金分割。黄金比例又称黄金分割，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1:0.618或1.618:1。0.618被公认为最具有审美意义的比例数字，这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域，而且在管理、工程设计等方面也有着不可忽视的作用。因此被称为黄金分割。斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….（从第三个数开始，后边每一个数都是前两个数的和）。然后我们会发现，随着斐波那契数列的递增，前后两个数的比值会越来越接近0.618，利用这个特性，我们就可以将黄金比例运用到查找技术中。

相对于折半查找，一般将待比较的key值与第mid=（low+high）/2位置的元素比较，比较结果分三种情况：

（1）key值与第mid=（low+high）/2相等，mid位置的元素即为所求；

（2）key值大于第mid=（low+high）/2，则令 low=mid+1；

（3）key值小于第mid=（low+high）/2，则令high=mid-1。

斐波那契搜索也是二分查找的一种提升算法，通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率。同样地，斐波那契查找也属于一种有序查找算法。

简介斐波那契查找与折半查找很相似，他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1，及n=F(k)-1；开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1)，比较结果也分为三种：

（1）相等，则mid位置的元素即为所求；

（2）>，则low=mid+1，k-=2；

说明：low=mid+1说明待查找的元素在[mid+1,high]范围内，k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))=Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个，所以可以递归的应用斐波那契查找。

（3））f(x2)，则删去(x2，1]，反之删去[0，x1)。以L1记删去的区间，再对留下的区间L2取：

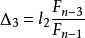
其中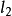， 为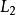 的长度。对L2重复上述步骤。如此反复直到：

已经证明，斐波那契搜索是一种函数估值次数最少的最优搜索方法1。

斐波那契搜索算法实现斐波那契搜索算法如下：

// 斐波那契查找.cpp #include "stdafx.h" #include #include using namespace std; const int max_size=20;//斐波那契数组的长度 /*构造一个斐波那契数组*/ void Fibonacci(int * F) { F[0]=0; F[1]=1; for(int i=2;iF[k]-1)//计算n位于斐波那契数列的位置 ++k; int * temp;//将数组a扩展到F[k]-1的长度 temp=new int [F[k]-1]; memcpy(temp,a,n*sizeof(int)); for(int i=n;i