[科普中国]-多元时间序列分析

多元时间序列分析(multivariate time series analysis)是指对多变量时间序列的研究。实际中，许多问题不仅是观察单个过程xt，而且是同时观察多个过程x1t，x2t，…，xrt，或者说xt为向量时，需要分析多变量时间序列xt=(x1t，x2t，…，xrt)T。例如，在工程上要研究电流与电压同时随时间变化的情况；在化学变化中要分析压力、温度和体积的变化关系；在气象预报分析时需要同时考虑该地区的雨量、气温和气压等记录资料。不仅要把他们各分量看做单变量过程来研究，而且要研究各分量之间的关系及变化规律，从而对时间序列做出预报和控制，这就是多元时间序列分析，其最典型的模型就是多元ARMA模型。

基本介绍实际中很多序列的变化规律都会受到其他序列的影响，比如在研究居民的人均消费序列时，由于消费会受收入的影响，如果能把收入也纳入研究范围，就能得到更精确的消费模型，这就涉及多元时间序列分析。1976年，Cox和Jenkins就采用天然气的输入速率作为输入变量，研究二氧化碳的输出浓度．这就将时间序列分析由一元推广到了多元的场合。但从技术上讲，当时要求输入序列和输出序列都是平稳的，显然这是非常苛刻的，进而限制了多元时间序列分析的应用。1987年Engle和Cranger提出了协整理论，在此理论下，并不要求响应序列和输入序列都平稳，只要求它们的回归残差序列平稳，这极大地促进了多元时间序列的发展，它实际上是将多元回归分析和时间序列****分析有机地结合在一起，有效地提高了预测精度1。

重要概念动态回归模型1976年Cox和Jenkins采用带输入变量的ARIMA模型，为平稳多元序列建模，该模型的构造思想是：假设响应序列和输人变量序列(即自变量序列)均平稳，首先构建响应序列和输入变量序列的回归模型：

式中，为第i个输入变量的自回归系数多项式，为第i个输入变量的移动平均系数多项式，为第i个输入变量的延迟阶数，为回归残差序列。

值得注意的是：回归模型不仅仅是关于的回归，也可以是关于的延迟变量的回归。

因为{}和均平稳，而且平稳序列的线性组合仍然是平稳的，所以残差序列为平稳序列：

使用ARMA模型继续提供残差序列{‘}中的相关信息，最终得到的模型为

该模型称为动态回归模型，简记为ARIMAX，式中为残差序列自回归系数多项式，为残差序列移动平均系数多项式，为零均值白噪声序列。

在ARIMAX模型中，如果平稳性条件不满足，就容易产生虚假回归的问题。我们考虑一元线性回归模型，为了检验模型的显著性，就需要对拟合模型进行检验：

假定响应序列和输入变量序列相互独立，理论上，检验结果应该接受原假设，如检验结果为拒绝，那么我们就接受了一个本不应该成立的回归模型，从而犯了第一类错误(纳伪错误)。由于样本的随机性，故纳伪错误会一直存在，我们可采用显著性水平控制纳伪错误的概率。

通常情况下，我们采用t统计量进行参数显著性检验：。当{}和{}都平稳时，该统计量服从自由度为样本容量的t分布，从而有

P(平稳序列)≤.

即当时，纳伪错误精确控制在内。

当{}和{}不平稳时，随机模拟的结果显示，检验统计量不服从t分布，这时t统计量的样本方差远远大于t分布的方差，如果仍采用t分布的临界值进行检验，拒绝原假设的概率就会大大增加，这样导致我们无法控制纳伪错误，容易接受本不该成立的回归模型，这种现象称为虚假回归1。

协整在现实生活中我们会发现，有些序列自身的变化虽然是非平稳的，但是序列与序列之间却具有非常密切地长期均衡关系，为了有效地衡量序列之间是否具有长期均衡关系，Engle和Granger 于1987 年提出了协整概念。

关于协整的含义，我们可以借助一个通俗的例子来加以解释。假设一男一女在舞厅里跳交谊舞，如果记录下男士和女士的活动轨迹，就得到了两条没有明显线性趋势的轨迹。虽然这两条轨迹都是非稳定的，但是却有一个关系是始终存在的：这两条轨迹始终受到某种规律的限制与联结(如遵照的舞曲)而保持同步。这种二者之间一起变化的关系可看作协整关系。联系到两个时间序列，尽管两个序列都是非平稳的，但它们的某种线性组合却可能是平稳的。例如消费和国民收人都是单位根过程，但变量却是平稳的。在这种情况下，我们称和是协整的，称为协整参数。

“协整”概念与经济学的“均衡”概念有本质上的联系。协整揭示了变量之间的一种长期稳定的均衡关系，是均衡关系在统计上的表述，因此在实证检验中用来判断变量间存在均衡关系的证据。比如，两个变量，虽然它们具有各自的长期波动规律，但如果它们是协整的，则它们之间存在着一个长期稳定的比例关系；反之，如果两个变量具有各自的长期波动规律，但它们不是协整的，则它们之间就不存在着一个长期稳定的比例关系。从图形上直观地讲，图1显示1966年至1993年间中国实际国民收入GNP的对数序列和实际消费C的对数序列的变化情况，两者很可能存在协整关系，而图2显示的两序列则随时间变化相距越来越远，不可能存在均衡关系。

结合单整概念，可得到关于协整的正式定义：如果序列都是d阶单整，存在一个向量，使得，其中b>0，，则认为序列是(d，b)阶协整，记为为协整向量。例如：国民收入时间序列为1阶单整序列，居民消费时间序列也为1阶单整序列，如果二者的线性组合构成的新序列为0阶单整序列，于是认为序列与是(1，1)阶协整。可见，如果两个变量都是单整变量，只有当它们的单整阶数相同时，才可能协整2。

EG检验多元非平稳序列之间能否建立动态回归模型，关键在于它们之间是否具有协整关系，因此要对多元非平稳序列建模，必须先进行协整检验，也称Engle-Granger，简称EG检验。由于自然界中绝大多数序列之间不具有协整关系，所以EG检验的假设条件如下确定：

：多元非平稳序列之间不存在协整关系；

：多元非平稳序列之间存在协整关系。

由于协整关系主要是通过考察回归残差的平稳性确定，所以上述假设条件等价于：

：回归残差序列非平稳↔：回归残差序列平稳．

EG检验也称为EG两步法，它遵循如下两个步骤：

步骤一：建立响应序列与输入序列之间的回归模型：

式中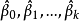是最小二乘估计值。

步骤二：对回归残差序列进行平稳性检验。

我们主要是采用单位根检验的方法来考察回归残差序列的平稳性，EG检验原理与计算公式的DF检验原理及计算公式相同，但是蒙特卡洛模拟的结果显示，它们的临界值略有不同，EG检验的临界值不仅与位移项、趋势项等因素有关，而且还与同归模型中非平稳变量的个数相关，Mackinnon提供了EG检验的临界值表，并将EG检验的临界值表与ADF检验的临界值表结合在一起。当非平稳序列的个数大于等于2时，对应的就是EG检验1。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学