[科普中国]-正规系统的不可判定性

正规系统的不可判定性是一种文法系统的不可判定特性。正规系统的判定问题是不可解的，由于以上问题是对所有的系统而言，故称为一般正规系统的判定问题。

简介正规系统的不可判定性是一种文法系统的不可判定特性。

所谓正规系统的判定问题是指：是否存在能行的算法，使得对任意的正规系统 S 及 S 上的两个字 W1W2，该算法可以判定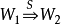是否成立。

可解性正规系统的判定问题是不可解的，由于以上问题是对所有的系统而言，故称为一般正规系统的判定问题。对具体的正规系统，也有其对应的特殊的判定问题，后者依赖于所给的系统。事实上，存在仅有两个字母组成的正规系统，其对应的特殊的判定问题是不可解的。1

算术系统的不可判定性(undecidability of ari-thmetic system)

佩亚诺算术系统的不可判定特性。

1936年，美国数学家、逻辑学家丘奇(Church,A.)用哥德尔证明不完备定理的思想证明了佩亚诺算术的不可判定性。美国学者罗塞(Rosser } J. B.)同年证明了佩亚诺算术是本质不可判定的。由算术系统的本质不可判定性还可以得到诸如 ZF系统等重要理论的不可判定性。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学