[科普中国]-追逃对策

基本介绍

追逃对策(pursuit-evasion game)是双方对追及与否的对策，一类典型的定性微分对策。参与对策的追、逃两方，分别记为P和E，P方欲迫近E，E方相反，欲远离P，若P方接近到E方的一定范围，并用ψ(x)≤0(目标集)表示，则称“追及”或“捕获”，这时对策结束1。

目标集(termination set)是一种集合，是定性微分对策结束时所要求实现的集合。在定性微分对策中，对策结束时所要求实现的条件界定的集合，如用导弹拦截飞机，要求在拦截过程结束时，飞机处于导弹爆炸时能击毁飞机的有效范围内，亦即导弹与飞机间的距离不超过某一给定值。一般地，目标集可写成ψ(x)≤0。

详细介绍追踪对策现象在军事上是经常出现的，例如，歼击机与轰炸机的战斗： 敌方的轰炸机要轰炸我方的目标，我方的歼击机为保卫这些目标，必须在轰炸机进人目标的轰炸有效范围之前打掉它或至少赶走它。此时，对策是由双方驾驶员进行的。也有不是人直接指挥的追踪对策，例如，反导弹跟踪弹道导弹就是靠导弹内部的自动控制装置指挥的。在追踪对策中追逃双方是在空间或地面运动的。这里逃的一方有时不是单纯逃，而是企图在被追到以前达到某种目的(例如达到有效轰炸的目的)。而追的一方就要在逃方达到那么，对于追踪问题我们应该怎样来研究呢? 微分对策提供了一种思路。让我们来看一个有趣的例子。

设想有一只老鼠在圆湖边碰上了猫，它想回洞已来不及，只好跳人湖中企图逃走。但猫在岸上跑的速度比鼠在湖中游的速度快得多,例如是鼠速的4 倍。粗看起来，老鼠没有好办法，只有束手就擒。但是，仔细研究一下，老鼠还是可以跑掉的。我们将老鼠所跑路线的奥妙介绍如下。

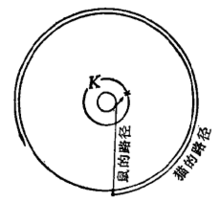
图1中大圆表示圆湖，其半径设为R，取,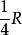为半径作一同心小圆K (我们将看到这是很有意思的区域)，于是老鼠跳人湖中后，先游到小圆K内，然后转圈游，猫在岸上按图中的路线跟着老鼠；但用同样的时间，老鼠在圆K内转圈所转过的角度比猫沿湖岸转圈转过的角度要大。所以老鼠可以游到和猫不在同一半径，而在同一直径的圆K的边界点*的位置上去，然后沿此直径游向湖岸。因为*点到湖岸的最短距离是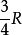设鼠的速度为v，则鼠由*点到湖岸所需的时间是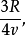由于猫的位置同*点不在同一半径上，所以猫到达同一地点的路程正好是半圆周，即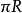。那么，猫的速度虽是鼠的4 倍(即4v)，但猫所需时间是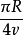，而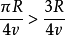 ，所以鼠先上岸，且有时间迅速跑入附近的鼠洞而溜掉。因此鼠确实有逃掉的办法，此也即为鼠的最优策略。所以发现这个有意思的小圆很重要。自然会问，对于一般追踪问题，存不存在这样或那样的有意思的区域呢? 同样会问，各种初始情况下，追逃双方的最优策略是什么? 微分对策的理论，就是提供一些思路来帮助人们找到这些问题的答案2。

根本要素追踪问题也存在对策现象所共有的根本要素：

局中人此时局中人就是追者与逃者，例如在空战中是一方的歼击机和另一方的轰炸机，在空防中是攻方的轰炸机和守方的高射炮，在导弹战中是一方的导弹和另一方的反导弹等等。

策略追逃双方都有自己的可选择的行动方案，例如轰炸机可选择飞行路线和投弹方式等，歼击机可选择迎击时间，飞行路线和攻击方式等，高射炮可选择发射角度等等。不过在追踪问题中局中人的完整的行动方案(即所谓策略)比矩阵对策中的完整的行动方案要复杂得多了。因为在追踪问题中，局中人例如歼击机必须每时每刻都掌握双方的相对位置和某些情况以便跟踪追击。同样轰炸机也得每时每刻都能掌握双方的相对位置和某些情况以便躲过攻击，飞达轰炸目标。所以用数学描述追踪对策中的策略，也必须要反映出这种连续动态的决策过程。这就得借助微分方程的理论，因此这类对策理论称为微分对策。

在微分对策中,通常用向量X(t)表示时刻t 时各方为继续进行对策所必须知道的双方的状况的量，例如空战中双方飞机的相对位置和机头所指方向等等，因此X(t)也被称为状况变量。

同时，各局中人都有控制自己运动路线的手段，例如飞机驾驶员可以做改变机速和使机头拐弯等操作，于是机速和机头拐弯的曲率半径等是属于局中人直接可控的量，这些量的改变就能引起前述状况变量的改变，并且这些量将怎么变，对方是不知道的，所以这些量称做控制量。

于是局中人的一个策略就是决定一个连续控制的规律,即对任意状况变量X(t) 给出自己应选的控制量。所以控制规律就是状况变量的函数，记为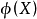(对追者)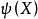，(对逃者)。

一般，当控制规律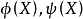为各方选定以后，双方的运动情况可由某个微分方程组描述：

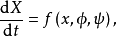此方程组也称为运动方程。

从理论上说，当给定了初始状况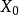和控制规律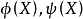后，由运动方程可解出双方在这局对策中自始至终的运动路线2。

一局对策的得失对于追踪对策，当追着了或逃掉了，即到达运动路线的终点时，这局对策也就结束了。但在终点上的得失不光是追着或逃掉，因为有时逃者并非单纯逃，而是企图在被追到以前达到某种目的。那么，追者必须在逃者达到目的之前追着它才是最好的。所以数学上应根据双方的目的，对得失(下面称作支付)作出不同的描述。例如：

(1) 如果关心的是能否追着，那么支付就可以用追着的时间来描述，没追着就对应于追着时间为无穷大或大于某个时刻T(即追者因动力燃料限制不能无限追下去)。支付这样描述时，追者是要尽快追着，即极小化追着的时间，而逃者则要极大化追着的时间。

(2) 如果关心的是进不进入某目标的邻域，那么支付可用追着时离目标邻域的距离来描述。此时保卫此目标者要极大化此距离，而袭击此目标者则要极小化这个距离。

总之在追踪问题中，对得失作出恰当的量的描述之后，总是一方要极大化这个量，而另一方则要极小化这个量。所以，在追踪问题中以极大极小原则定义最优策略，也是很令人信服的2。

解决这一类问题，可运用连续函数的运动学微分方程求解：

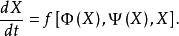
式中为追方的控制函数关系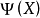，为逃方的控制函数关系，X是描写追逃双方相互位置的状态变量。若能给定初条件，则可解该方程以求得双方的运动路线。