[科普中国]-固定模

定义

考虑一个具有N个局部控制站的大规模线性时不变系统：

式中：分别表示为系统状态向量，第控制站的输入向量和输出向量。其原始系统的控制和输出阶次为m和 r ，由以下(3)给定

和是具有相应阶次的实常数矩阵。

分散镇定问题就是要找出N个具有动态补偿器的局部输出控制规律：

使整个系统稳定。式中是第 i 个补偿器的输出向量，是 i 控制器外部输入向量， 矩阵分别为。或者说，分散输出镇定是要决定，使得由(1)和(2)所描述的闭环系统其极点在复平面预定的集合之中。

定义1 考虑由(1)和(2)所描述的系统及整数。令的增益矩阵K代表下述对角方块矩阵集合中的矩阵：

这里。那么系统对于K的“固定多项式”就是对所有，多项式集合的最大公共因子，并用下式表示：

定义2 对系统和由(4)所给定的输出反馈的集合，那么对于K的的固定模的集合定义为矩阵特征值所有可能集合的交集，即

式中表示特征值的集合。我们注意到，K可以取零矩阵，因此，固定模的集合包含于。根据定义(1)，固定模即是式(5)中固定多项式的根，即

{|和} (6)

式中S表示在整个S复平面上点的集合。

寻求固定模的方法戴维逊用以下的算法，提供了快速寻求系统固定模的方法。

步骤1 求所有A的特征值，即。

步骤2 选择任意矩阵(用伪随机数发生器或其它方法)使表示矩阵的范数。

步骤3 求的特征值。

步骤4 对于K的，即的固定模包含在与A的特征值相同的特征值之中。

步骤5 重复上述步骤4，直到止的固定模完全确定为止。

可以证明：集中系统的固定模，这里是，即相应于系统不可控和不可观测的模。

有了固定多项式和固定模的概念之后，就可以导出分散闭环系统稳定的充分和必要条件。

相关定理定理1 对于式(1)和式(2)所描述的系统和式(4)那种类型的对角方决矩阵K， 当且仅当固定模的集合包含在S复平面的左半开平面，即

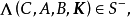式中表示S复平面的左半开平面，那么式(3)所表示的局部反馈规律才能使系统渐近稳定。2