[科普中国]-转移函数

基本释义

把具有线性特性的对象的输入与输出间的关系，用一个函数（输出波形的拉普拉斯变换与输入波形的拉普拉斯变换之比）来表示的，称为转移函数。原是控制工程学的用语，在生理学上往往用来表述心脏、呼吸器官、瞳孔等的特性。

系统的转移函数与描述其运动规律的微分方程是对应的。可根据组成系统各单元的转移函数和它们之间的联结关系导出整体系统的转移函数，并用它分析系统的动态特性、稳定性，或根据给定要求综合控制系统，设计满意的控制器。以转移函数为工具分析和综合控制系统的方法称为频域法。它不但是经典控制理论的基础，而且在以时域方法为基础的现代控制理论发展过程中，也不断发展形成了多变量频域控制理论，成为研究多变量控制系统的有力工具。转移函数中的复变量s在实部为零、虚部为角频率时就是频率响应。

转移函数也是《积分变换》里的概念。对复参数s，函数f(t)*e^(-st)在（-∞，+∞）的积分，称为函数f(t)的（双边）拉普拉斯变换，简称拉氏变换（如果是在[0,+∞)内积分，则称为单边拉普拉斯变换，记作F(s)，这是个复变函数。

设一个系统的输入函数为x(t），输出函数为y(t)，则y(t)的拉氏变换Y(s)与x(t)的拉氏变换X(s)的商：W(s)=Y(s)/X(s)称为这个系统的转移函数。

转移函数是由系统的本质特性确定的，与输入量无关。知道转移函数以后，就可以由输入量求输出量，或者根据需要的输出量确定输入量了。

转移函数的概念在自动控制理论里有重要应用。

推导简单说明一下，下面的描述都是以复数 s = σ + j*ω 为变量的。在许多应用中，足以限定 σ=0 (于是 s = j*ω)，从而将含有复参数的拉普拉斯变换简化为实参 ω 的傅里叶变换。

那么，对于最简单的连续时间输入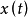信号 和输出信号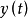 来说，转移函数 所反映的就是零状态条件下输入信号的拉普拉斯变换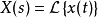 与输出信号的拉普拉斯变换 之间的线性映射关系：

或者在离散时间系统中，应用Z变换，转移函数可以类似地表示成这常常被称为脉冲转移函数。

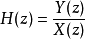
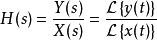
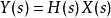
从微分方程直接推导考虑一个常系数线性微分方程

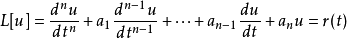其中u和r是t的适当的光滑函数。L是相关函数空间上定义的，将u变换为r的算子。这种方程可以用于以强迫函数r为变量约束输出函数u。转移函数写成算子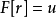的形式，是L的右逆，因为。

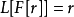这个常系数齐次微分方程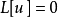的解可以通过尝试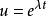找到。这个代换会产生特征多项式

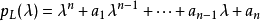
在输入函数r的形式也为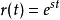的时候，非齐次的情形也可以很容易的解决。在那种情况下，通过代入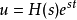就可以发现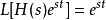当且仅当

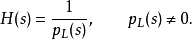
把那当作转移的定义需要注意区分实数和复数的差异。这是受到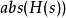表示增益，而用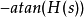表示相位滞后惯例的影响。转移函数的其他定义还有例如。

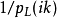性质1、转移函数是一种数学模型，与系统的微分方程相对应。

2、是系统本身的一种属性，与输入量的大小和性质无关。

3、只适用于线性定常系统。

4、转移函数是单变量系统描述，外部描述。

5、转移函数是在零初始条件下定义的，不能反映在非零初始条件下系统的运动情况。

6、一般为复变量 S 的有理分式，即 n ≧ m。且所有的系数均为实数。

7、如果转移函数已知，则可针对各种不同形式的输入量研究系统的输出或响应。

8、如果转移函数未知，则可通过引入已知输入量并研究系统输出量的实验方法，确定系统的转移函数。

9、转移函数与脉冲响应函数一一对应，脉冲响应函数是指系统在单位脉冲输入量作用下的输出。

应用转移函数主要应用在三个方面。

1、 确定系统的输出响应。对于转移函数G(s)已知的系统，在输入作用u(s)给定后，系统的输出响应y(s)可直接由G(s)U(s)运用拉普拉斯反变换方法来定出。

2、分析系统参数变化对输出响应的影响。对于闭环控制系统，运用根轨迹法可方便地分析系统开环增益的变化对闭环转移函数极点、零点位置的影响，从而可进一步估计对输出响应的影响。

3、用于控制系统的设计。直接由系统开环转移函数进行设计时，采用根轨迹法。根据频率响应来设计时，采用频率响应法。