频率变换(frequency transformation)是设计滤波器的一种方法,把一个频带范围变换到另一个相应的频带范围,称之为频率变换。利用频率变换可设计各种类型的频率选择滤波器。其基本思想是:根据给定的待设计指标,先变换成相应的低通原型滤波器的设计指标;然后按照低通滤波器的设计方法,设计出一个低通原型波滤器;最后再通过频率变换,求得所要求的实际低通、高通、带通或带阻滤波器,频率变换有模拟频率变换与数字频率变换,可根据设计对象的要求来选取1。
基本介绍基于低通原型滤波器的综合设计方法得到的表格和曲线是设计实际滤波器的基础,但不能直接套用,这是因为实际滤波器与低通原型滤波器存在两方面的差异:一是衰减特性和频率尺度不同,二是元件的数值和性质的不同。因此,要利用低通原型滤波器的设计表格和曲线来设计实际的滤波器,首先须将实际滤波器的衰减特性通过频率变换,成为低通原型滤波器的衰减特性;然后查找低通原型滤波器的表格和曲线,求得低通原型滤波器的归一化元件值,再利用等衰减条件和频率变换,求出实际滤波器的归一化元件值;最后进一步求出实际滤波器的真实元件值。
可见,要利用低通原型滤波器的现成设计表格和曲线求实际滤波器的真实元件值,既要用到频率变换又要用到等衰减条件。所谓频率变换,就是将低通原型的衰减特性的(角)频率变量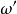 变换为实际滤波器的(角)频率变量
变换为实际滤波器的(角)频率变量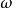 ,而等衰减条件则可借助图1所示的两个结构相似的梯形网络导出。图中两种结构的信源内阻和负载均为纯电阻,且其值不随频率的变化而变化。在图1(a)中,信源角频率为
,而等衰减条件则可借助图1所示的两个结构相似的梯形网络导出。图中两种结构的信源内阻和负载均为纯电阻,且其值不随频率的变化而变化。在图1(a)中,信源角频率为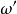 ,梯形网络各支路的阻抗为
,梯形网络各支路的阻抗为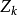 ;在图1(b)中,信源角频率为
;在图1(b)中,信源角频率为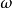 ,各支路阻抗为
,各支路阻抗为 ,如果这两个梯形网络各支路的阻抗一一相等。即
,如果这两个梯形网络各支路的阻抗一一相等。即
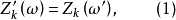 则它们具有相同的衰减,上式就是等衰减条件。
则它们具有相同的衰减,上式就是等衰减条件。

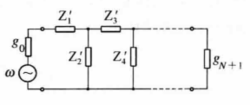
根据等衰减条件下的频率变换,即可通过低通原型滤波器的归一化元件值分别求得四类滤波器的真实元件值。下面介绍低通原型滤波器向低通滤波器、高通滤波器的频率变换2。
低通滤波器实际低通滤波器真实元件值的确定可按以下四个步骤进行。
(a)频率变换
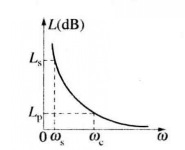
设实际的和原型的低通滤波器的频率变量分别为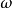 和
和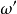 ,两者的衰减特性如图2所示。要求在频率为
,两者的衰减特性如图2所示。要求在频率为 的点上分别对应于
的点上分别对应于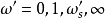 ,两者的衰减量L彼此
,两者的衰减量L彼此
相等,由此可得到频率变换: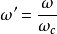 。
。
(b)查图表和曲线得到低通原型的归一化元件值。
(c)求实际低通滤波器的归一化元件值
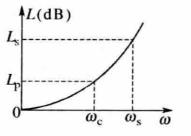
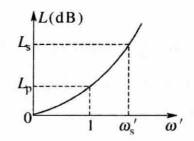
图3(a)和(b)分别示出了原型的和实际的低通滤波器的电路结构,欲使这两种滤波器有相等的衰减特性,根据式(1),应有
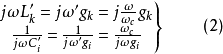 式中,下标k为串联元件标号,i为并联元件标号,它们分别取奇数和偶数。由此得到实际低通滤波器的归一化元件值为
式中,下标k为串联元件标号,i为并联元件标号,它们分别取奇数和偶数。由此得到实际低通滤波器的归一化元件值为
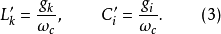
(d)求实际低通滤波器的真实元件值
求实际低通滤波器的真实元件值,只需对信源内阻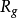 进行反归一化即可得到
进行反归一化即可得到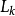 和
和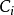 ,即
,即
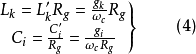
而实际负载则由原型电路的负载性质确定。若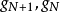 并联。则
并联。则
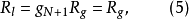 若
若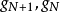 串联,则
串联,则
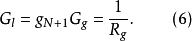
以上讨论的是电感输入式电路的情况,对电容输入式电路,上述分析同样适用,只是串联元件标号k与并联元件标号 互换。此外,确定实际低通滤波器真实元件值的步骤同样适用于其他三类滤波器2。
互换。此外,确定实际低通滤波器真实元件值的步骤同样适用于其他三类滤波器2。
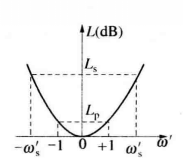
高通滤波器借助于频率变换,可将低通原型滤波器的频率特性转换为高通滤波器的频率特性。此时,可采用以下的频率变换函数:
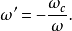 式中,
式中,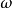 为高通滤波器的频率变量,
为高通滤波器的频率变量,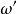 为低通原型的频率变量,两者的衰减频率特性分别如图3(a)和(b)所示。这样,基于等衰减条件,即可由低通原型滤波器设计表格中查出的归一化元件值
为低通原型的频率变量,两者的衰减频率特性分别如图3(a)和(b)所示。这样,基于等衰减条件,即可由低通原型滤波器设计表格中查出的归一化元件值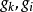 ,通过转换得到电感输入式低通原型电路对应的高通滤波器电路的归一化电感
,通过转换得到电感输入式低通原型电路对应的高通滤波器电路的归一化电感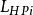 和电容
和电容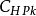 值。高通滤波器电路结构中的电感和电容将取代电感输入式低通原型滤波器电路中的并联电容和串联电感的位置,
值。高通滤波器电路结构中的电感和电容将取代电感输入式低通原型滤波器电路中的并联电容和串联电感的位置,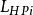 和
和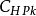 (仍记为
(仍记为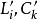 )的值应按以下公式计算:
)的值应按以下公式计算:
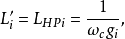
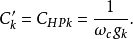
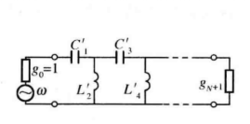
式中,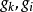 分别为低通原型滤波器电路中的电感和电容对应的g值。通过电感输入式低通原型电路转换得到的对应高通滤波器电路如图3(c)所示。
分别为低通原型滤波器电路中的电感和电容对应的g值。通过电感输入式低通原型电路转换得到的对应高通滤波器电路如图3(c)所示。
这样,实际的电感输入式高通滤波器的电路结构中的电感和电容的真实元件值分别为
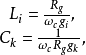 而负载电阻
而负载电阻 。
。
类似地,对电容输入式低通原型转换得到的高通滤波器,其对应电路同样可根据电容输入式低通原型滤波器电路画出,而其归一化电感和归一化电容值以及对应的真实值与低通原型的归一化元件值之间同样满足上述关系,只是需将相关参数的下标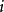 和
和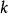 互换。
互换。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国