[科普中国]-三角插值

概念

插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。常用的插值方法有多项式插值、样条差值、分段插值、三角插值等。

而三角插值，作为常用的插值方法之一，是指取插值函数为三角多项式的插值方法。特别适用于对周期函数的插值.设被插值函数f(x)为以2二为周期的函数，取n阶三角多项式称上式为高斯三角插值公式1。

相关定理定理1设函数f的周期函数为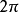 、且具有连续的一阶导数，则Fourier级数 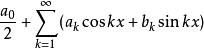一致收敛于f。其中系数有下列公式计算：

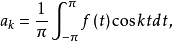
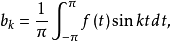显然系数满足 。

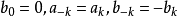定理2Flourier级数定理）

设，则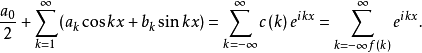

三角多项式在数学中，三角多项式是一类基于三角函数的函数的总称。三角多项式是可以表示成有限个正弦函数sin(nx) 和余弦函数cos(nx) 的和的函数，其中的x是变量，而n是一个自然数。三角多项式中每一项的系数可以是实数或者复数。如果系数是复数的话，那么这个三角多项式是一个傅里叶级数。

三角多项式在许多数学分支，如数学分析和数值分析中都有应用，例如在傅里叶分析中，三角多项式被用于傅里叶级数的表示，在三角插值法中，三角多项式被用于逼近周期性函数2。

定义一个函数T如果能够写成：

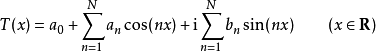的形式，其中对于所有的 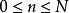，an和bn都是复数，那么就称其为N阶复三角多项式。运用欧拉公式，这个函数可以写为：

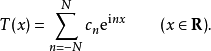同样地，如果对于所有的{\displaystyle 0\leq n\leq N}，an和bn都是实数的话，那么函数t

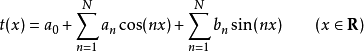就被称N阶实三角多项式。

性质是关于的n次多项式,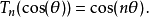 实际上，这种多项式称为第一类切比雪夫多项式。同样地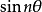， 也是关于 和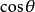 的n次多项式，称为第二类切比雪夫多项式。

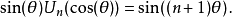因此，一个三角多项式实际上也可以认为是关于三角函数 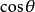和 的多项式。

三角多项式都是周期为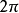 的周期函数。同时，任何连续的周期函数都可以借助于三角多项逼近到任意接近的程度。

应用（费耶三角插值）在傅利叶谱分析中 ，一旦函数 f 的狄利克雷和系数通过在等距节点处的数值求积确定下来 ，结果函数就在这些点处插值 f 并以高精度逼近连续部分和 。 通过研究三角多项式和立方样条差值逼近连续费耶和问题 ，可以得到以下结果 ：连续费耶和可以通过两个费耶插值的平均以高精度逼近 ，一个在偶指标结点集插值 f ，另一个在奇指标结点集插值 f ，由于立方样条插值容易构造 ，所以它常被用来代替三角插值 。

傅里叶和并不对所有连续函数收敛 ，而费耶和对所有连续函数都收敛 ，三角插值理论的几个过程都可以通过费耶和的方式得到 ，大多数情况下这些多项式的一致收敛性也可以通过对应的多项式显示形式直接得到 。由可和函数的费耶定理可以得到一个重要事实 ，即 ：所有可和函数均由其傅里叶系数唯一确定 。

许多人研究过三角插值求和表明 ，在许多情况下 ，傅利叶级数的每个收敛或可和性理论 ，都可以移植到等距节点的三角插值过程的收敛性或可和性 ，这一类型的算子可看作离散算子的特例3 。