高斯方程是子流形的基本方程。第一基本型和第二基本型构成曲面的完全不变量系统。即: 如果两张曲面有相同的第一基本型和第二基本型,则它们在三维欧几里得空间的一个刚体运动下能够完全重合。
简介在曲面的正交参数系(即F= 0)下高斯方程是
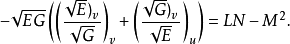 在曲面上取正交曲率线网作为参数曲线网(即
在曲面上取正交曲率线网作为参数曲线网(即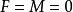 )时,科达齐方程是
)时,科达齐方程是
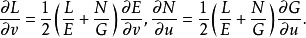
给定两个二次微分形式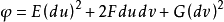 和
和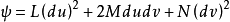 ,假定
,假定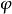 是正宗的,如果它们满足高斯方程和科达齐方程,则在三维欧几里得空间中存在一张以
是正宗的,如果它们满足高斯方程和科达齐方程,则在三维欧几里得空间中存在一张以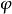 为他的第一基本型、以
为他的第一基本型、以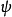 为它的第二基本型,并且这样的曲面至多差在空间中的位置不同是唯一确定的。这个定理称为曲面伦基本定理 (fundamental theorem for surface theory)。1
为它的第二基本型,并且这样的曲面至多差在空间中的位置不同是唯一确定的。这个定理称为曲面伦基本定理 (fundamental theorem for surface theory)。1
第二基本型[second fundamental form]
定义正则参数曲面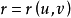 上的二次微分式
上的二次微分式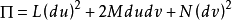 称为曲面的第二基本型(也称为第二基本形式),其中
称为曲面的第二基本型(也称为第二基本形式),其中
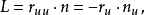
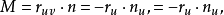
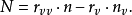
几何意义第二基本型的直观几何意义是:曲面上点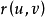 的邻近点
的邻近点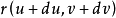 到曲面在点
到曲面在点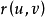 处的切平面的有向距离近似等于
处的切平面的有向距离近似等于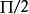 ,即
,即
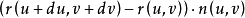
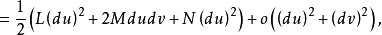 式中,
式中,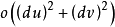 是高于
是高于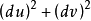 的无穷小量。
的无穷小量。
应用第一基本型和第二基本型合在一起用来描述三维欧儿里得空间中曲面的形状和大小,由此派生出曲面的各种曲率的概念,见法曲率,主曲率、中曲率和高斯曲率等。
另外,第一基本型和第二基本型构成曲面的完全不变量系统。即:如果两张曲面有相同的第一基本型和第二基本型,则它们在三维欧几里得空间的一个刚体运动下能够完全重合。
但是曲面的第一基本型和第二基本型不是彼此独立的,它们之间有深刻的内在联系。通常把曲面的第一基本型和第二基本型所满足的关系式称为高斯方程(Gauss equation) 和科达齐方程(Codazzi equations)。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国