极小曲面方程(minimal surface equation)是在固定边界上的具有最小面积的曲面所满足的方程。设Rn+1中的曲面方程为xn+1=u(x)(x∈Ω),则面积积分S=∫Ω√(1+|Du|2)dx的欧拉-拉格朗日方程Mu=(1/n)Di((Diu)/(1+|Du|2))1/2=0即是极小曲面方程。这是一个熟知的拟线性椭圆型方程,它是更一般的指定平均曲率方程的特例。若Ω是Rn中的有界C2区域,则狄利克雷问题Mu=0(在Ω内),u=φ(在∂ Ω上)对任意φ∈C0(∂ Ω)有解的充分必要条件是边界∂ Ω的平均曲率处处非负1。
定义表述1 极小曲面方程(minimal surface equation)是偏微分方程和微分几何中的一个非常重要的方程,它是极小曲面所满足的微分方程。设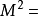 {
{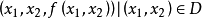 ,D为
,D为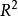 中的一区域}为
中的一区域}为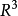 中的一极小曲面,由于
中的一极小曲面,由于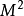 的平均曲率为零,所以有
的平均曲率为零,所以有
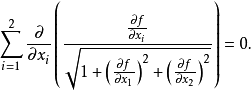 此方程称为极小曲面方程2。
此方程称为极小曲面方程2。
表述2 设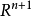 中的曲面方程为
中的曲面方程为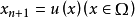 ,则面积积分
,则面积积分
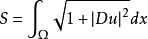 的欧拉-拉格朗日方程
的欧拉-拉格朗日方程
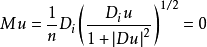 即是极小曲面方程。这是一个熟知的拟线性椭圆型方程,它是更一般的指定平均曲率方程的特例。若Ω是
即是极小曲面方程。这是一个熟知的拟线性椭圆型方程,它是更一般的指定平均曲率方程的特例。若Ω是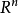 中的有界
中的有界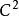 区域,则狄利克雷问题
区域,则狄利克雷问题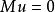 (在Ω内),
(在Ω内),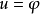 (在∂ Ω上)对任意
(在∂ Ω上)对任意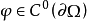 有解的充分必要条件是边界∂ Ω的平均曲率处处非负1。
有解的充分必要条件是边界∂ Ω的平均曲率处处非负1。
相关分析(接表述1)一般地,设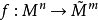 为一极小浸入,局部地由
为一极小浸入,局部地由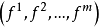 所给出。换言之,相对于M中的坐标系
所给出。换言之,相对于M中的坐标系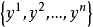 及
及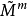 中的坐标系
中的坐标系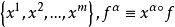 ,若
,若
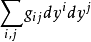 及
及
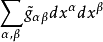 局部地为
局部地为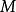 及
及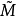 上的度量,则
上的度量,则
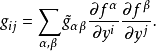 因为M是极小的,所以对M中每一幺正基
因为M是极小的,所以对M中每一幺正基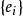 ,有
,有
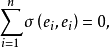 或等价地
或等价地
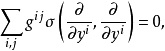 其中
其中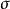 为M的第二基本形式。将上式详细写出来,得
为M的第二基本形式。将上式详细写出来,得
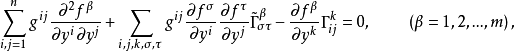 其中
其中
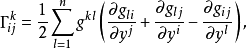
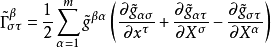 分别为M及
分别为M及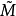 的联络系数,这是一个拟线性的椭圆型方程组。若
的联络系数,这是一个拟线性的椭圆型方程组。若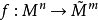 是黎曼流形间的一个极小浸入,则函数
是黎曼流形间的一个极小浸入,则函数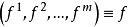 必适合上述方程组2。
必适合上述方程组2。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国