[科普中国]-蒙日一安培方程

蒙日一安培方程是一类从黎曼几何问题中提出来的二阶完全非线性偏微分方程，同时也是卡拉比-丘流形证明时曾用的工具。蒙日一安培方程由于其完全非线性的特性使得其求解一直是一个困难的问题。蒙日一安培方程的应用十分广泛，在微分几何、变分法、最优化问题及传输问题等领域均有应用。

数学表示定义两个非独立变量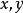，以及一个独立变量，蒙日-安培方程可以表述为：

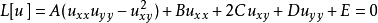这里的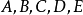为一阶变量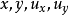，是唯一的非独立函数。

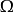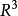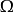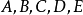Rellich定理是一个的有界区域，在上是关于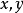的连续函数，蒙日-安培方程的狄利克雷问题可以表示为：

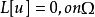
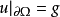
如果有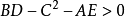，那么这个狄利克雷问题至多两个解。1

椭圆型蒙日-安培方程如果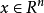，且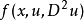是一个正值函数，那么蒙日-安培方程：

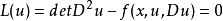是一个完全非线性椭圆型偏微分方程。

应用该方程在微分几何、变分法、最优化问题及传输问题等领域有广泛应用。2在通过图像的匹配进行搜索时，输入一个图像，在网上寻找最相近的图像。黑白照片由灰黑色点组成，可以看成是一个概率分布：该点的颜色越黑，就认为该点的概率密度越大。于是两张照片匹配问题就转化为两个概率分布的匹配问题。1991年，白罗尼发现，如果这两个分布都是连续分布，那么这个匹配对应的可以写成一个梯度映射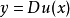，其中是一个凸函数，且满足著名的蒙日-安培方程。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学