三级数定理是概率论中判定随机变量和的序列几乎处处收敛的重要定理。三级数定理给出了随机变量和序列几乎处处收敛的必要条件和充分条件。
简介三级数定理是关于独立随机变量和的几乎处处收敛的判定定理。1
必要条件设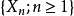 是独立随机变量序列,那么使得级数
是独立随机变量序列,那么使得级数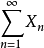 几乎处处收敛的必要条件是对每个常数c
几乎处处收敛的必要条件是对每个常数c (0,
(0,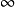 )
)
(1)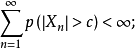
(2)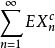 收敛;
收敛;
(3)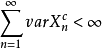 .
.
充分条件充分条件是对某一个常数c (0,
(0,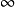 ),上述三级数收敛。
),上述三级数收敛。
充分必要条件三级数定理是关于独立随机变量和的收敛定理,设(ξn,n≥1) 是独立随机变量列,则
 几乎必然收敛的充分必要条件是:对于某一固定的常数 c>0,下列三个级数收敛:
几乎必然收敛的充分必要条件是:对于某一固定的常数 c>0,下列三个级数收敛:
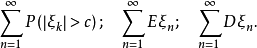 其中
其中
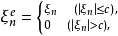 为ξn 在 c 处的截尾。
为ξn 在 c 处的截尾。
几乎处处收敛定义在测度空间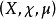 上的函数列
上的函数列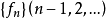 及f,如果
及f,如果
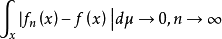 则称
则称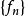 平均收敛于f,记为
平均收敛于f,记为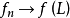 。
。
假若下面的关系式成立:对任意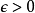 ,
,
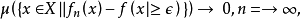 则称
则称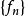 依测度 μ 收敛(convergence in measureμ)于 f,记为
依测度 μ 收敛(convergence in measureμ)于 f,记为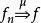 。若在X的一个
。若在X的一个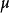 测度为0的子集外,对
测度为0的子集外,对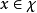 ,均有
,均有
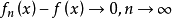 则称
则称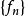 则称关于测度μ几乎处处收敛于 f ,记为
则称关于测度μ几乎处处收敛于 f ,记为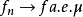 。
。
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国