定义
我们知道,随机变量实际上是定义在概率空间上取值为实数的函数,因此我们可以像数学分析时论函数序列逐点收敛性那样去讨论随机变量序列在每个样本点处取值的收敛性。然而,由于随机变量取值的随机性,我们常常不可能期待随机变量序列在所有样本点处都存在极限,现在的问题是研究极限是否在一个概率为1的点集上存在。
设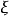 和
和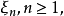 是定义在概率空间
是定义在概率空间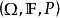 上的随机变量。
上的随机变量。
1. 如果存在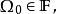 使得
使得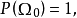 且对任意
且对任意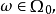 有
有 则称
则称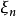 以概率****1收敛(converges with probability one)或几乎必然收敛(converges almost surely)于
以概率****1收敛(converges with probability one)或几乎必然收敛(converges almost surely)于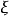 ,记作
,记作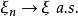 。
。
2. 如果存在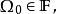 使得
使得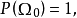 且对任意
且对任意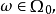 数列
数列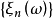 是柯西基本列,即
是柯西基本列,即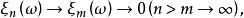 则称
则称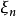 以概率1是柯西基本列。
以概率1是柯西基本列。
注: 以概率1收敛意味着最多除去一个零概率事件外,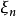 逐点收敛于
逐点收敛于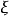 ,根据柯西基本列一定存在极限的原则
,根据柯西基本列一定存在极限的原则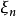 以概率1收敛当且仅当
以概率1收敛当且仅当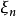 以概率1是柯西基本列。1
以概率1是柯西基本列。1
以概率1收敛的判别准则下面给出以概率1收敛的判别准则。
定理设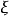 和
和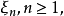 是定义在概率空间
是定义在概率空间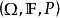 上的随机变量
上的随机变量
(1) 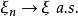 当且仅当对任意
当且仅当对任意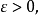
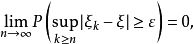 或者等价地
或者等价地
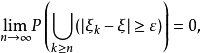
(2) 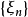 以概率1是柯西基本列当且仅当对任意
以概率1是柯西基本列当且仅当对任意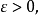
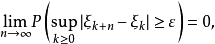 或者等价地
或者等价地
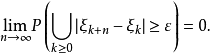
定理证明(1)对任意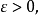 令
令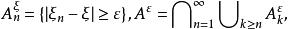 那么
那么
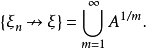
由连续性定理
 于是下列关系式成立
于是下列关系式成立
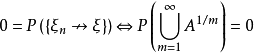
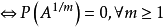
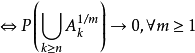

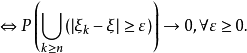 (2) 对任意
(2) 对任意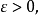 令
令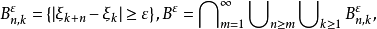 那么事件
那么事件
{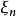 不是柯西基本列}=
不是柯西基本列}=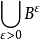 .
.
推论如果对任意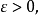
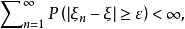 则
则
 **证明:**注意到
**证明:**注意到
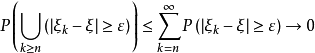 即可。1
即可。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国