[科普中国]-跳跃条件

流体流动出现内部间断（如激波）时，此处微分方程失去了意义，需要用间断面两侧各力学量之间物理上存在的关系，即Rankine-Hugoniot条件作为特殊的边界条件，称为跳跃条件。它作为流动的内边界条件并保证解的唯一性所必须。

Rankine-Hugoniot条件，也称为Rankine-Hugoniot跳跃条件或Rankine-Hugoniot关系，描述了流体中一维流动中冲击波两侧的状态与固体中的一维变形之间的关系。 他们被认定为苏格兰工程师和物理学家威廉·约翰·麦克康兰金和法国工程师皮埃尔·亨利·胡戈尼奥（Pierre Henri Hugoniot）所开展的工作。另见Salas（2006）有一些历史背景。1

在与冲击相关的坐标系中，兰金 - 胡格诺维尔条件可以表示为：

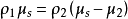
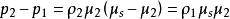
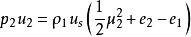这里是冲击波速度，ρ1和ρ2是冲击后面和内部的流体的质量密度，u2是冲击内流体的粒子速度，p1和p2是两个区域中的压力，e1和 e2是两个区域的特定（每单位质量的感觉）内部能量。 这些等式可以从下面的等式（12），（13）和（14）中直接导出。 使用兰金 - 胡戈尼奥方程来保存质量和动量以消除我们和u2，能量守恒方程可以表示为Hugoniot方程：

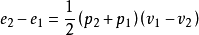其中v1和v2分别是每单位质量的未压缩和压缩的特定体积。

考虑一维容器（例如，长细管）中的气体。 假设流体是非粘性的（即，其不显示粘度效应，例如与管壁摩擦）。2 此外，假设没有传导或辐射的热传递，并且可以忽略重力加速度。 这样一个系统可以通过以下的守恒定律来描述，称为1D欧拉方程，其保护形式是：

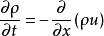
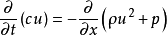
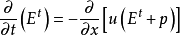
在这里，ρ是流体质量密度[kg / m3]

u 是流体速度[m / s]

e 是流体的特定内部能量，[J / kg]

p是流体压力，[Pa]

t是时间，[s]

x是距离，[m]

是流体的总能量密度[J / m3]，而e是其特定内部能量[焦耳/千克]。

进一步假设气体是热量理想的，因此是简单形式的多变方程状态。3

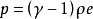是有效的，其中 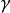是比热的恒定比例 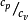。 该数量也表现为多变指数。

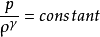
关于可压缩流动方程的广泛列表等，请参阅NACA报告1135（1953）。

注意：对于热量理想的气体γ是一个常数，对于热理想气体γ是温度的函数。 在后一种情况下，压力对质量密度和内部能量的依赖性可能与等式给出的不同。

在继续进行之前，有必要引入跳跃条件的概念 - 这种条件是不连续或突然变化的。4

考虑一维情况，其中标量保守的物理量w跳跃，由积分守恒定律

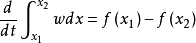对于x1，x2，因为x1