开关曲线是使时间最优控制函数改变符号的曲线。二阶时间最优控制系统的状态空间是二维欧几里得平面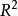 (或是
(或是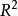 中包含原点为内点的某区域
中包含原点为内点的某区域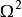 ),对于控制作用是标量的情况,如果一条通过坐标原点的曲线
),对于控制作用是标量的情况,如果一条通过坐标原点的曲线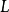 把相平面
把相平面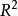 分为两部分
分为两部分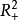 和
和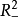 (或把
(或把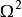 分为两部分
分为两部分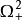 和
和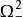 ),即
),即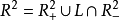 (或
(或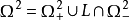 ),使得在
),使得在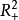 (或
(或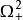 )内最优控制取正值,在
)内最优控制取正值,在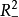 (或
(或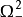 )内最优控制取负值,在曲线
)内最优控制取负值,在曲线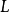 上,最优控制的取值亦是完全确定的,并且经过原点的那段
上,最优控制的取值亦是完全确定的,并且经过原点的那段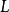 必定是时间最优轨线,则称曲线
必定是时间最优轨线,则称曲线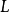 是时间最优控制系统的开关曲线。当控制作用是二维向量时,时间最优控制系统有两条开关曲线。这样,二阶线性定常受控系统的时间最优控制的综合在于求得其开关曲线1。
是时间最优控制系统的开关曲线。当控制作用是二维向量时,时间最优控制系统有两条开关曲线。这样,二阶线性定常受控系统的时间最优控制的综合在于求得其开关曲线1。
Bang-Bang控制又叫开关控制或快速控制。实质上是最优控制的一种特殊形式——时间最优控制。常规的PID反馈系统,通常是以被控变量的最大超调量,偏差的积分面积等等作为评定控制品质的指标,而Bang-Bang控制则是被控变量从一个状态到另一个状态的时间最短为其品质指标。系统设计的核心问题是设计开关函数。根据开关函数及系统的状态,决定控制作用是正向作用还是反向作用。它虽然可以看成是一种位式调节,但显然与一般位式调节有明显不同,是因为它引进了时间最优的概念,它的切换不仅受调节偏差控制,而且受偏差的微分信号控制,因而可以避免位式控制超调量大的弊病。另外,开关控制还有一个稳定的工作点,即当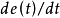 及
及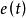 均为零,执行机构不动作2。
均为零,执行机构不动作2。
举例说明如下:已知对象特性曲线为
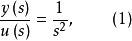 控制作用的不等式约束为:
控制作用的不等式约束为: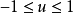 ,实际上执行机构以
,实际上执行机构以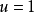 与
与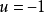 两位(开关)控制。
两位(开关)控制。
设计步骤如下:
为求对象的开关函数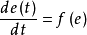 或
或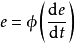 ,将对象特性记为
,将对象特性记为
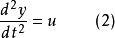 或记为
或记为
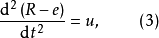 因为对于定值调节系统
因为对于定值调节系统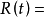 常数,所以上式可写成
常数,所以上式可写成
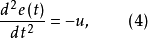 如果定义如下变量:
如果定义如下变量:
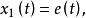
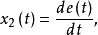 则(4)式可写成
则(4)式可写成
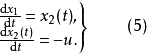
为了求开关函数,分别将 代人(5)式,当
代人(5)式,当 时,可解出
时,可解出
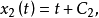
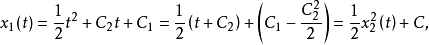 或记作为
或记作为
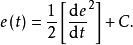 同样将
同样将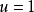 代人可推出
代人可推出
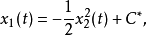 或记作为
或记作为
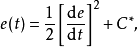 其中C与C*由初始条件决定。
其中C与C*由初始条件决定。
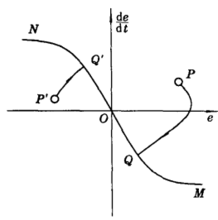
图1表示了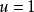 与
与 的两簇曲线,通常称通过坐标原点的曲线
的两簇曲线,通常称通过坐标原点的曲线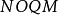 为开关曲线。
为开关曲线。
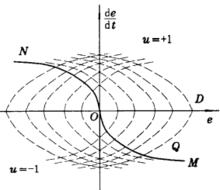
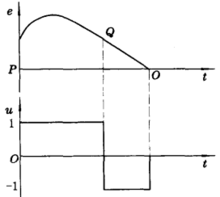
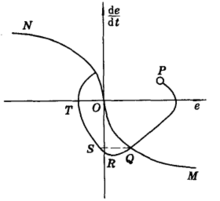
控制要求是系统在某一初始状态P点,在开关作用下,经最短时间回到零点(即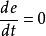 )而稳定下来。由图2知,不论初始状态如何,最终必然要转移到开关曲线
)而稳定下来。由图2知,不论初始状态如何,最终必然要转移到开关曲线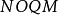 上,然后再沿开关曲线回到原点,若初始状态在
上,然后再沿开关曲线回到原点,若初始状态在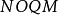 上(如P点),则系统控制作用保持
上(如P点),则系统控制作用保持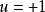 ,直到达到OM曲线为止,开关才变换方向,使控制作用变为
,直到达到OM曲线为止,开关才变换方向,使控制作用变为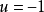 并一直保持到平衡点。当初始状态在
并一直保持到平衡点。当初始状态在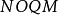 之下(如P’点)系统的控制作用一直保持为
之下(如P’点)系统的控制作用一直保持为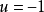 ,直到ON曲线为止,开关才变换方向使控制作用变为
,直到ON曲线为止,开关才变换方向使控制作用变为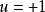 ,并一直保持到终点。可见,在对象为二阶系统时,开关作用的符号只改变一次,一般而言,若对象为n阶要实现最优控制,开关作用将至多切换
,并一直保持到终点。可见,在对象为二阶系统时,开关作用的符号只改变一次,一般而言,若对象为n阶要实现最优控制,开关作用将至多切换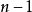 次,显然,此时若想如二阶系统那样确定改变控制作用的转换曲线(开关曲线)就不那么简单。因为要确定n维状态空间中转曲面(开关曲面)就困难。更何况确定了转换曲面后,还得研究状态轨迹,并确定切换点(或切换时间)。
次,显然,此时若想如二阶系统那样确定改变控制作用的转换曲线(开关曲线)就不那么简单。因为要确定n维状态空间中转曲面(开关曲面)就困难。更何况确定了转换曲面后,还得研究状态轨迹,并确定切换点(或切换时间)。
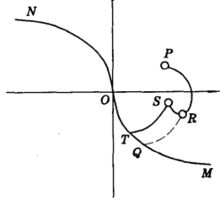
比较图3(a)、(b)中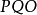 轨迹与
轨迹与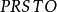 轨迹,可以看出
轨迹,可以看出 轨迹时间最短。
轨迹时间最短。
从实际观点出发,为简化算法,我们可以用一直线方程近似地表示抛物线开关曲线,这时所得到的系统就不再是最佳的,但它是很接近于最佳系统的。
开关控制系统每计算调节一次,都需要检测控制偏差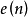 ,并计算其微分,
,并计算其微分,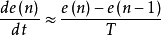 ,判断系统状态是在开关曲线上方、下方或处于开关曲线上,若在开关曲线上方,则实行
,判断系统状态是在开关曲线上方、下方或处于开关曲线上,若在开关曲线上方,则实行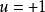 的控制;若在开关曲线的下方,则实行
的控制;若在开关曲线的下方,则实行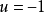 的控制;若在原点上,则
的控制;若在原点上,则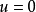 。每次动作后状态轨迹与开关曲线相交,立即改变控制方向。根据上述解释可作出Bang-Bang控制程序框图,图略2。
。每次动作后状态轨迹与开关曲线相交,立即改变控制方向。根据上述解释可作出Bang-Bang控制程序框图,图略2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国