[科普中国]-正态概率纸

简述

正态概率纸是一种具有特殊刻度的坐标纸，它能使正态变量的取值x和对应的分布函数值F(x)组成的数对(x，F(x))在这张概率纸上呈现出一条直线。众所周知在一般直角坐标系中，正态分布函数的图形是一条曲线，而且不少分布函数的图形也有类似的形状，因此从曲线形状上来判断正态性非常困难，而在正态概率纸上，只有正态分布函数的图形是直线，其他分布函数的图形是曲线，这就大大提高了判断正态分布的能力。2

利用正态概率纸对质量数据进行分析，与直方图相比具有信息量大、解决问题更迅速的优点，特别适宜在现场使用。

利用正态概率纸来检验总体的正态性，方法简易、直观，不过结论往往比较粗略，有时，作结论时不同人员还可能发生争议，尽管如此，此法仍有较大的实用价值。3

构造原理设总体X有分布函数： 表示正态分布族，需要检验假设 。

这里，μ和σ²均为未知参数，在原假设为真时，通过中心化变换

即：

服从正态N(0,1)。函数u(x)是x线性函数，在[x,u(x)]直角坐标平面上是一条直线，这条直线过点(μ,0)，且斜率为1/σ。

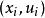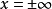为了便于应用，在平面上不标出点，而直接标出，我们以横轴上的刻度表示x；在纵轴上，先刻出u的刻度(均匀)，而后根据u的值，从正态N(0,1))分布表中查出对应的分布函数φ(u)，刻在u的位置上(不均匀)。例如在u=2的位置上刻上97.72(%)，u=1的位置上刻上84.13(%)，u=0的位置上刻上50(%)等。然后把u的刻度抹去，留下x与F(%)的刻度就构成一张正态概率图纸。由于正态分布在中连续变化，而又不能在图纸上表出的点，所以常用的正态概率纸的纵辅刻摩隔千从0.01到99.99。4

使用步骤1、收集数据作频数分布表。

2、计算经验分布概率。

3、在正态概率纸上确定横座标，确定原则与作直方图时相同。

4、在横座标上确定各组组中值的位置，相对应在纵座标上确定分布概率值，二者一一对应得到若于个点，连接各点画成直线或曲线。

5、计算和分析。

1).各点连接，若近似为一条直线，说明基本符合正态分布，若呈曲线则说明不符合正态分布；

2).直线与对应纵坐标50%的水平线相交点的横座标刻度值即为；

3).直线与对应纵坐标84%(σ)的水平线相交点的横座标刻度值与的差即为标准偏差S。5

用途与频率直方图相比，使用正态概率纸免去大量的计算工作，所以，在判断统计数据是否服从正态分布时，可以用正态概率纸代替频率直方图。正态概率纸除了用来判断统计数据是否服从正态分布外，还用于：

①检查统计数据中是否存在离群值；

②求样本总体平均值μ和总体标准偏差σ的估计值；

③求统计数据的极差R；

④求过程能力指数Cp和Cpk；

⑤估计不合格品率；

⑥求偏移量ε和公差中心M。6