正则条件概率(The regular conditional probability)亦称条件概率测度。
定义设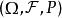 为概率空间,
为概率空间,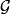 为
为 的子
的子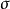 代数。由条件期望的性质知:
代数。由条件期望的性质知:
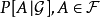 具有以下性质:
具有以下性质:
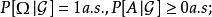
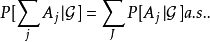
这些性质与概率测度的性质(全空间的测度等于1,非负性,可数可加性)很相似,不同之处在于出现了例外集.
假定对于每一个集合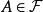 ,我们取定
,我们取定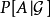 的一个版本
的一个版本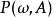 (即
(即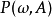 为
为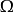 上的一个确定的
上的一个确定的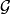 可测函数,并且
可测函数,并且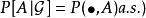 .我们希望去掉一个例外集(概率为零)
.我们希望去掉一个例外集(概率为零)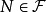 使得,对于任意的
使得,对于任意的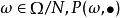 为
为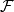 上的一个概率测度:非负性及在全空间上的值等于1不成问题,只需要它满足可数可加性:即对于任意可数个两两不相交的集合
上的一个概率测度:非负性及在全空间上的值等于1不成问题,只需要它满足可数可加性:即对于任意可数个两两不相交的集合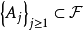 ,必须有下式成立
,必须有下式成立
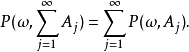 但是,根据条件期望的定义,我们只知道
但是,根据条件期望的定义,我们只知道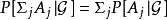 。因此,对于每一个集合序列
。因此,对于每一个集合序列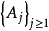 ,需要去掉一个例外集
,需要去掉一个例外集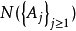 才能使得式
才能使得式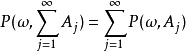 成立;而这样的序列个数通常都是不可数的,我们知道不可数个零概集的并集不一定还是零概集(其实并起来的集合是否属于
成立;而这样的序列个数通常都是不可数的,我们知道不可数个零概集的并集不一定还是零概集(其实并起来的集合是否属于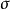 代数
代数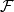 我们都不知道,即并起来的集合的可测性我们一般都不知道).如果能够去掉一个公共的零概集N,使得式
我们都不知道,即并起来的集合的可测性我们一般都不知道).如果能够去掉一个公共的零概集N,使得式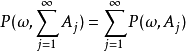 成立,可在N上,对于任意集合
成立,可在N上,对于任意集合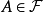 ,定义
,定义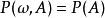 ,则式
,则式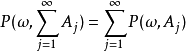 对所有
对所有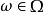 成立。
成立。
设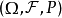 为一概率空间,
为一概率空间,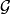 为
为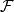 的子
的子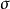 代数.令
代数.令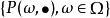 为
为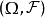 上的一族概率测度,称它为P关于
上的一族概率测度,称它为P关于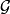 的正则条件概率,如果
的正则条件概率,如果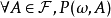 为
为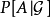 的一个版本,即以下两个条件成立:
的一个版本,即以下两个条件成立:
(1)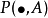 为
为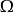 上的
上的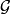 可测函数;
可测函数;
(2)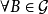 ,
,
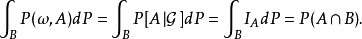
相关定理定理1:设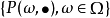 为P关于
为P关于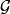 的正则条件概率。设X为一随机变量,其期望存在,则对几乎所有
的正则条件概率。设X为一随机变量,其期望存在,则对几乎所有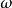 ,X关于概率测度
,X关于概率测度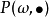 的积分存在,并且有
的积分存在,并且有
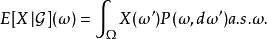 证明 :从示性可测函数过渡到非负可测函数,再到一般可测函数(随机变量) 。
证明 :从示性可测函数过渡到非负可测函数,再到一般可测函数(随机变量) 。
该定理表明,有了正则条件概率,条件期望可以看做是关于条件概率的积分。
定理2: 设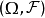 为一可分可测空问,P为
为一可分可测空问,P为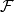 上的一紧概率测度,则对
上的一紧概率测度,则对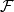 的任一子
的任一子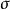 代数
代数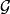 ,存在P关于
,存在P关于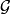 的正则条件概率。
的正则条件概率。
定理3:设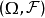 为一Radon可测空间,P为
为一Radon可测空间,P为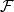 上的一概率测度,则对
上的一概率测度,则对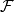 的任一子
的任一子 代数
代数 ,存在P关于
,存在P关于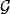 的正则条件概率。1
的正则条件概率。1
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国